Conformal Prediction in Julia

Conformal Prediction in Julia

Part 1 — Introduction

Figure 1: Prediction sets for two different samples and changing coverage rates. As coverage grows, so does the size of the prediction sets. Image by author.

A first crucial step towards building trustworthy AI systems is to be transparent about predictive uncertainty. Model parameters are random variables and their values are estimated from noisy data. That inherent stochasticity feeds through to model predictions and should to be addressed, at the very least in order to avoid overconfidence in models.

Beyond that obvious concern, it turns out that quantifying model uncertainty actually opens up a myriad of possibilities to improve up- and down-stream modelling tasks like active learning and robustness. In Bayesian Active Learning, for example, uncertainty estimates are used to guide the search for new input samples, which can make ground-truthing tasks more efficient (Houlsby et al. 2011). With respect to model performance in downstream tasks, uncertainty quantification can be used to improve model calibration and robustness (Lakshminarayanan, Pritzel, and Blundell 2016).

In previous posts we have looked at how uncertainty can be quantified in the Bayesian context (see here and here). Since in Bayesian modelling we are generally concerned with estimating posterior distributions, we get uncertainty estimates almost as a byproduct. This is great for all intends and purposes, but it hinges on assumptions about prior distributions. Personally, I have no quarrel with the idea of making prior distributional assumptions. On the contrary, I think the Bayesian framework formalises the idea of integrating prior information in models and therefore provides a powerful toolkit for conducting science. Still, in some cases this requirement may be seen as too restrictive or we may simply lack prior information.

Enter: Conformal Prediction (CP) — a scalable frequentist approach to uncertainty quantification and coverage control. In this post we will go through the basic concepts underlying CP. A number of hands-on usage examples in Julia should hopefully help to convey some intuition and ideally attract people interested in contributing to a new and exciting open-source development.

📖 Background

Conformal Prediction promises to be an easy-to-understand, distribution-free and model-agnostic way to generate statistically rigorous uncertainty estimates. That’s quite a mouthful, so let’s break it down: firstly, as I will hopefully manage to illustrate in this post, the underlying concepts truly are fairly straight-forward to understand; secondly, CP indeed relies on only minimal distributional assumptions; thirdly, common procedures to generate conformal predictions really do apply almost universally to all supervised models, therefore making the framework very intriguing to the ML community; and, finally, CP does in fact come with a frequentist coverage guarantee that ensures that conformal prediction sets contain the true value with a user-chosen probability. For a formal proof of this marginal coverage property and a detailed introduction to the topic, I recommend the tutorial by Angelopoulos and Bates (2021).

In what follows we will loosely treat the tutorial by Angelopoulos and Bates (2021) and the general framework it sets as a reference. You are not expected to have read the paper, but I also won’t reiterate any details here.

CP can be used to generate prediction intervals for regression models and prediction sets for classification models (more on this later). There is also some recent work on conformal predictive distributions and probabilistic predictions. Interestingly, it can even be used to complement Bayesian methods. Angelopoulos and Bates (2021), for example, point out that prior information should be incorporated into prediction sets and demonstrate how Bayesian predictive distributions can be conformalised in order to comply with the frequentist notion of coverage. Relatedly, Hoff (2021) proposes a Bayes-optimal prediction procedure. And finally, Stanton, Maddox, and Wilson (2022) very recently proposed a way to introduce conformal prediction in Bayesian Optimisation. I find this type of work that combines different schools of thought very promising, but I’m drifting off a little … So, without further ado, let us look at some code.

📦 Conformal Prediction in Julia

In this section of this first short post on CP we will look at how conformal prediction can be implemented in Julia. In particular, we will look at an approach that is compatible with any of the many supervised machine learning models available in MLJ: a beautiful, comprehensive machine learning framework funded by the Alan Turing Institute and the New Zealand Strategic Science Investment Fund. We will go through some basic usage examples employing a new Julia package that I have been working on: ConformalPrediction.jl.

ConformalPrediction.jl is a package for uncertainty quantification through conformal prediction for machine learning models trained in MLJ. At the time of writing it is still in its early stages of development, but already implements a range of different approaches to CP. Contributions are very much welcome:

Documentation

Contributor’s Guide

Split Conformal Classification

We consider a simple binary classification problem. Let (Xᵢ, Yᵢ), i=1,…,n denote our feature-label pairs and let μ: 𝒳 ↦ 𝒴 denote the mapping from features to labels. For illustration purposes we will use the moons dataset 🌙. Using MLJ.jl we first generate the data and split into into a training and test set:

using MLJ 
using Random Random.seed!(123)  

# Data:
X, y = make_moons(500; noise=0.15) 
train, test = partition(eachindex(y), 0.8, shuffle=true)

Here we will use a specific case of CP called split conformal prediction which can then be summarised as follows:

1. Partition the training into a proper training set and a separate calibration set: 𝒟ₙ=𝒟[train] ∪ 𝒟[cali].
2. Train the machine learning model on the proper training set: μ(Xᵢ, Yᵢ) for i ∈ 𝒟[train].
3. Compute nonconformity scores, 𝒮, using the calibration data 𝒟[cali] and the fitted model μ(Xᵢ, Yᵢ) for i ∈ 𝒟[train].
4. For a user-specified desired coverage ratio (1-α) compute the corresponding quantile, q̂, of the empirical distribution of nonconformity scores, 𝒮.
5. For the given quantile and test sample X[test], form the corresponding conformal prediction set: C(X[test])={y: s(X[test], y) ≤ q̂}

This is the default procedure used for classification and regression in ConformalPrediction.jl.

You may want to take a look at the source code for the classification case here. As a first important step, we begin by defining a concrete type SimpleInductiveClassifier that wraps a supervised model from MLJ.jl and reserves additional fields for a few hyperparameters. As a second step, we define the training procedure, which includes the data-splitting and calibration step. Finally, as a third step we implement the procedure in the equation above (step 5) to compute the conformal prediction set.

The permalinks above take you to the version of the package that was up-to-date at the time of writing. Since the package is in its early stages of development, the code base and API can be expected to change.

Now let’s take this to our 🌙 data. To illustrate the package functionality we will demonstrate the envisioned workflow. We first define our atomic machine learning model following standard MLJ.jl conventions. Using ConformalPrediction.jl we then wrap our atomic model in a conformal model using the standard API call conformal_model(model::Supervised; kwargs...). To train and predict from our conformal model we can then rely on the conventional MLJ.jl procedure again. In particular, we wrap our conformal model in data (turning it into a machine) and then fit it on the training set. Finally, we use our machine to predict the label for a new test sample Xtest:

# Model:
KNNClassifier = @load KNNClassifier pkg=NearestNeighborModels 
model = KNNClassifier(;K=50)   

# Training:
using ConformalPrediction 
conf_model = conformal_model(model; coverage=.9) 
mach = machine(conf_model, X, y) 
fit!(mach, rows=train)  

# Conformal Prediction:
Xtest = selectrows(X, first(test)) 
ytest = y[first(test)] 
predict(mach, Xtest)[1]

> UnivariateFinite{Multiclass{2}}     
     ┌ ┐ 
   0 ┤■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ 0.94   
     └ ┘

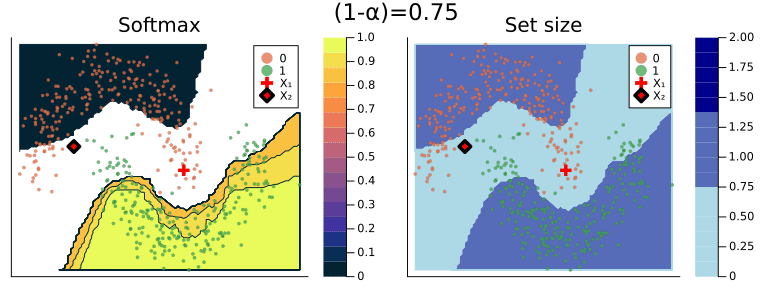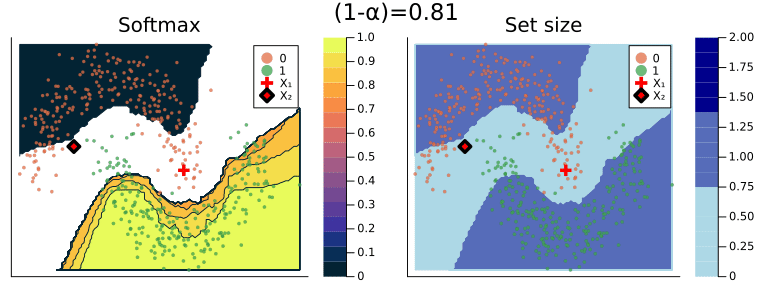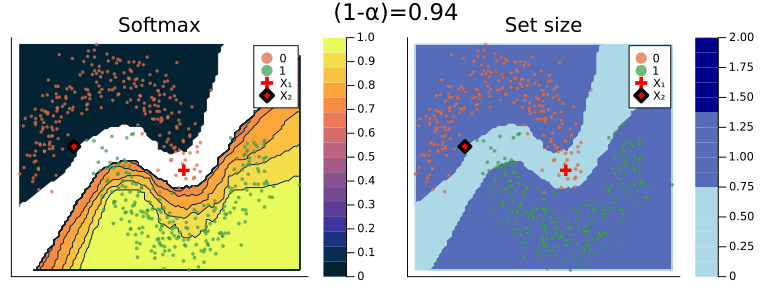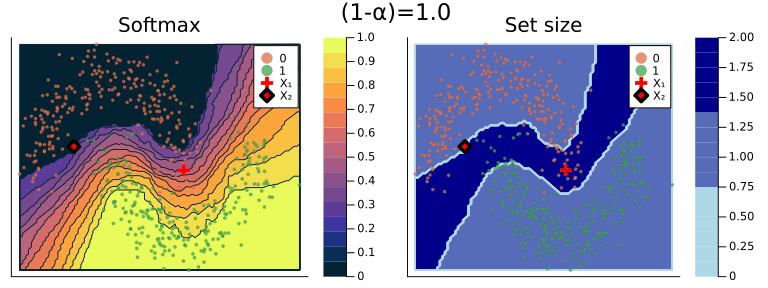
The final predictions are set-valued. While the softmax output remains unchanged for the SimpleInductiveClassifier, the size of the prediction set depends on the chosen coverage rate, (1-α).

When specifying a coverage rate very close to one, the prediction set will typically include many (in some cases all) of the possible labels. Below, for example, both classes are included in the prediction set when setting the coverage rate equal to (1-α)=1.0. This is intuitive, since high coverage quite literally requires that the true label is covered by the prediction set with high probability.

conf_model = conformal_model(model; coverage=coverage) 
mach = machine(conf_model, X, y) 
fit!(mach, rows=train)  

# Conformal Prediction:
Xtest = (x1=[1],x2=[0]) 
predict(mach, Xtest)[1]

> UnivariateFinite{Multiclass{2}}    
     ┌ ┐ 
   0 ┤■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ 0.5   
   1 ┤■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ 0.5   
     └ ┘

Conversely, for low coverage rates, prediction sets can also be empty. For a choice of (1-α)=0.1, for example, the prediction set for our test sample is empty. This is a bit difficult to think about intuitively and I have not yet come across a satisfactory, intuitive interpretation (should you have one, please share!). When the prediction set is empty, the predict call currently returns missing:

conf_model = conformal_model(model; coverage=coverage) 
mach = machine(conf_model, X, y) 
fit!(mach, rows=train)  

# Conformal Prediction: 
predict(mach, Xtest)[1]

> missing

Figure 2 should provide some more intuition as to what exactly is happening here. It illustrates the effect of the chosen coverage rate on the predicted softmax output and the set size in the two-dimensional feature space. Contours are overlayed with the moon data points (including test data). The two samples highlighted in red, X₁ and X₂, have been manually added for illustration purposes. Let’s look at these one by one.

Firstly, note that X₁ (red cross) falls into a region of the domain that is characterized by high predictive uncertainty. It sits right at the bottom-right corner of our class-zero moon 🌜 (orange), a region that is almost entirely enveloped by our class-one moon 🌛 (green). For low coverage rates the prediction set for X₁ is empty: on the left-hand side this is indicated by the missing contour for the softmax probability; on the right-hand side we can observe that the corresponding set size is indeed zero. For high coverage rates the prediction set includes both y=0 and y=1, indicative of the fact that the conformal classifier is uncertain about the true label.

With respect to X₂, we observe that while also sitting on the fringe of our class-zero moon, this sample populates a region that is not fully enveloped by data points from the opposite class. In this region, the underlying atomic classifier can be expected to be more certain about its predictions, but still not highly confident. How is this reflected by our corresponding conformal prediction sets?

Well, for low coverage rates (roughly <0.9) the conformal prediction set does not include y=0: the set size is zero (right panel). Only for higher coverage rates do we have C(X₂)={0}: the coverage rate is high enough to include y=0, but the corresponding softmax probability is still fairly low. For example, for (1-α)=0.9 we have p̂(y=0|X₂)=0.72.

These two examples illustrate an interesting point: for regions characterised by high predictive uncertainty, conformal prediction sets are typically empty (for low coverage) or large (for high coverage). While set-valued predictions may be something to get used to, this notion is overall intuitive.

Figure 2: The effect of the coverage rate on the conformal prediction set. Softmax probabilities are shown on the left. The size of the prediction set is shown on the right. Image by author.

🏁 Conclusion

This has really been a whistle-stop tour of Conformal Prediction: an active area of research that probably deserves much more attention. Hopefully, though, this post has helped to provide some color and, if anything, made you more curious about the topic. Let’s recap the most important points from above:

1. Conformal Prediction is an interesting frequentist approach to uncertainty quantification that can even be combined with Bayes.
2. It is scalable and model-agnostic and therefore well applicable to machine learning.
3. ConformalPrediction.jl implements CP in pure Julia and can be used with any supervised model available from MLJ.jl.
4. Implementing CP directly on top of an existing, powerful machine learning toolkit demonstrates the potential usefulness of this framework to the ML community.
5. Standard conformal classifiers produce set-valued predictions: for ambiguous samples these sets are typically large (for high coverage) or empty (for low coverage).

Below I will leave you with some further resources.

📚 Further Resources

Chances are that you have already come across the Awesome Conformal Prediction repo: Manokhin (n.d.) provides a comprehensive, up-to-date overview of resources related to the conformal prediction. Among the listed articles you will also find Angelopoulos and Bates (2021), which inspired much of this post. The repo also points to open-source implementations in other popular programming languages including Python and R.

References

Angelopoulos, Anastasios N., and Stephen Bates. 2021. “A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification.” https://arxiv.org/abs/2107.07511.

Hoff, Peter. 2021. “Bayes-Optimal Prediction with Frequentist Coverage Control.” https://arxiv.org/abs/2105.14045.

Houlsby, Neil, Ferenc Huszár, Zoubin Ghahramani, and Máté Lengyel. 2011. “Bayesian Active Learning for Classification and Preference Learning.” https://arxiv.org/abs/1112.5745.

Lakshminarayanan, Balaji, Alexander Pritzel, and Charles Blundell. 2016. “Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles.” https://arxiv.org/abs/1612.01474.

Manokhin, Valery. n.d. “Awesome Conformal Prediction.”

Stanton, Samuel, Wesley Maddox, and Andrew Gordon Wilson. 2022. “Bayesian Optimization with Conformal Coverage Guarantees.” https://arxiv.org/abs/2210.12496.

For attribution, please cite this work as:

Patrick Altmeyer, and Patrick Altmeyer. 2022. “Conformal Prediction in Julia 🟣🔴🟢.” October 25, 2022.

Originally published at https://www.paltmeyer.com on October 25, 2022.