Introduction
At some point, students of the finite element method need to come to grips with sparse matrices. The finite element method is really viable only if it results in sufficiently sparse matrices. Firstly due to the reduction of the memory needed to store the matrix to the point where the data can be accommodated by the current hardware limits, and secondly because of the attendant gains in performance as the zero entries need not be processed.
Classical finite element approaches lead to matrices that are sparse, symmetric, and positive definite. One of the established techniques to deal with a sparse matrix is to allocate storage for the matrix entries below the so called envelope (sometimes referred to as skyline). Only one triangle of the matrix needs to be stored (either the lower or the upper). Here we assume that in each column we need to store only the entries below the top nonzero in that column and the diagonal.
Due to the expected properties of the matrices as outlined above, either a Cholesky or an LDLT factorization of such matrices can be employed to solve a system of linear algebraic equations. Below we discuss the latter technique.
Gauss elimination
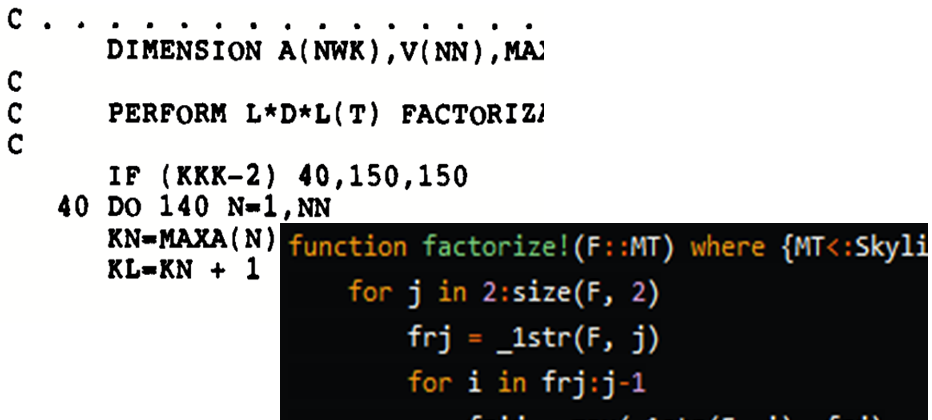
The textbook by Bathe1 describes a sophisticated version of the Gauss elimination which operates on the upper triangle of the matrix, producing the entries of the LT factor and the entries of the diagonal D. Figure 1 below is the complete description of the algorithm.
Figure 1: Active-column LDLT factorization.
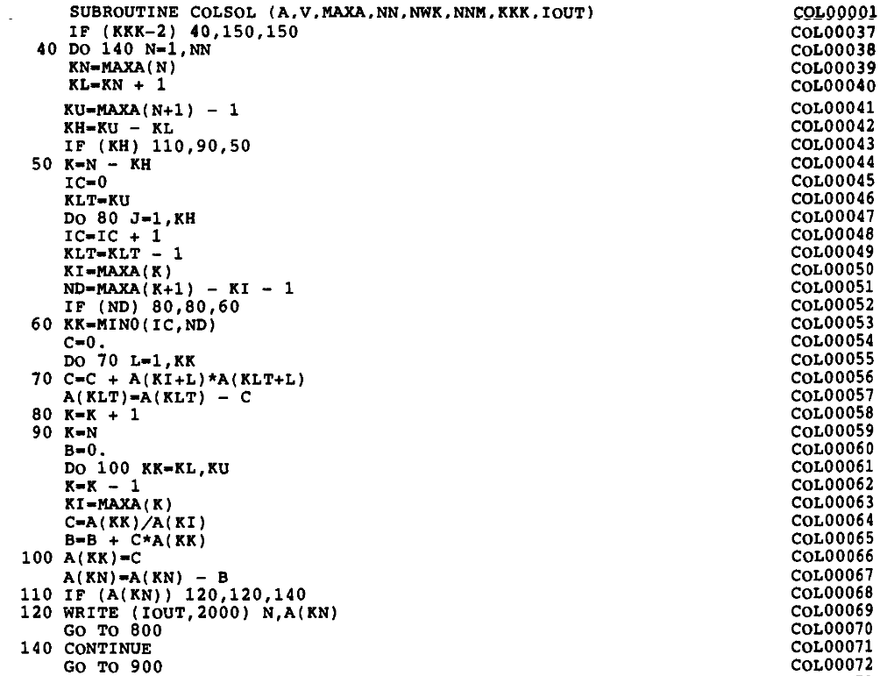
For a long time, the textbook by Bathe1 served as a reference of the implementation (page 448). Figure 2 shows the Fortran code of the envelope-matrix factorization (originally in Fortran IV, later modified to Fortran 77) from this book.
Figure 2: Fortran implementation of the active-column LDLT factorization.
Clearly, there is a wide chasm between the description of the algorithm and the code that implements it. Of course, the archaic form of the Fortran source (all those arithmetic if statements, and no indentation at all) may be partially at fault, but even if we rewrite the original Fortran code in Julia (function _colsol_factorize! in Figure 3), with proper indentation and such, the mapping of the algorithm to the code is not at all self-evident.
function _colsol_factorize!(a, maxa)
nn = length(maxa) - 1
for n in 1:nn
kn = maxa[n]
kl = kn + 1
ku = maxa[n+1] - 1
kh = ku - kl
if (kh > 0)
k = n - kh
ic = 0
klt = ku
for j in 1:kh
ic = ic + 1
klt = klt - 1
ki = maxa[k]
nd = maxa[k+1] - ki - 1
if (nd > 0)
kk = min(ic,nd)
c = 0.
for l in 1:kk
c = c + a[ki+l]*a[klt+l]
end
a[klt] = a[klt] - c
end
k = k + 1
end
end
if (kh >= 0)
k = n
b = 0.0
for kk in kl:ku
k = k - 1
ki = maxa[k]
c = a[kk]/a[ki]
b = b + c*a[kk]
a[kk] = c
end
a[kn] = a[kn] - b
end
if (a[kn] == 0)
@error "Zero Pivot"
end
end
end
Figure 3: Fortran code of Figure 2 rewritten in Julia.
Algorithm for dense matrices
If we momentarily disregard the need to operate on a sparse matrix, stored with the envelope method, and we write the algorithm of Figure 1 for a dense matrix, the Julia code shown in Figure 4 can be easily mapped one-to-one to the algorithm of Figure 1. The matrix F is a symmetric dense matrix, which gets overwritten in the upper triangle and the diagonal
with the factors.
function dense_ldlt!(F)
M = size(F, 1)
for j in 2:M
for i in 1:j-1
F[i, j] -= dot(F[1:i-1, i], F[1:i-1, j])
end
s = F[j, j]
for r in 1:j-1
t = F[r, j] / F[r, r]
s -= t * F[r, j]
F[r, j] = t
end
F[j, j] = s
end
F
end
Figure 4: Julia implementation of algorithm of Figure 1 for a dense matrix.
We do not use separate symbols for the final values of the entries (L) and their intermediates (g), as in algorithm in Figure 1, because the distinction is quite clear in the code. The first loop was replaced with a dot product, and the second loop was slightly rewritten in order to avoid duplicate calculation of the same quantity.
Algorithm for sparse matrices
The sparse matrix in the envelope form can be stored as follows:
struct SkylineMatrix{IT, T}
# Dimension of the square matrix
dim::IT
# The entries are ordered column-by-column, from
# the first non zero entry in each column down to the diagonal.
# This array records the linear index of the diagonal
# entry, `das[k]`, in a given column `k`.
# The `das[0]` address is for a dummy 0-th column.
das::OffsetVector{IT, Vector{IT}}
# Stored entries of the matrix
coefficients::Vector{T}
end
Figure 5: Type of a matrix stored using the envelope scheme.
The addressing of entries of the matrix is accomplished by storing indexes (addresses) of the diagonal entries of the matrix. Any other entry can be identified by the column and the indexes of the diagonal entry in the current and previous columns.
Thus, we can retrieve all entries in column c of the matrix sky, for the rows r between the first stored entry in the column and the diagonal, as
for r in _1str(sky, c):c
sky.coefficients[_co(sky.das, c) + r]
end
using the functions
_1str(sky, c) = sky.das[c-1] - _co(sky.das, c) + 1
which calculates the row index of the first stored entry in column c, and the helper function
_co(das, c) = das[c] - c
that calculates the offset of the entries for column c.
Julia provides much nicer facilities to express access to the matrix entries, however. In particular, we can define functions getindex as
function Base.getindex(sky::SkylineMatrix{IT, T}, r::IT, c::IT) where {IT, T}
sky.coefficients[_co(sky.das, c) + r]
end
and
function Base.getindex(sky::SkylineMatrix{IT, T}, r::UnitRange{IT}, c::IT) where {IT, T}
@views sky.coefficients[_co(sky.das, c) .+ (r)]
end
to define indexing with a single row subscript or a range of row subscripts. This allows us to write the access to all the values in column c as
for r in _1str(sky, c):c
sky[r, c]
end
or sky[_1str(sky, c):c, c].
When we need to set the value of an entry, we can define the function setindex!
function Base.setindex!(sky::SkylineMatrix{IT, T}, v::T, r::IT, c::IT) where {IT}
sky.coefficients[_co(sky.das, c) + r] = v
end
so that we can set for instance sky[r, c] += 1.0.
And so it is now possible to define the algorithm of Figure 1 applied to a sparse matrix as a very slight modification of the implementation for the dense matrix (refer to Figure 4):
function factorize!(F::MT) where {MT<:SkylineMatrix}
for j in 2:size(F, 2)
frj = _1str(F, j)
for i in frj:j-1
frij = max(_1str(F, i), frj)
if frij <= i-1
F[i, j] -= @views dot(F[frij:i-1, i], F[frij:i-1, j])
end
end
s = F[j, j]
for r in frj:j-1
t = F[r, j] / F[r, r]
s -= t*F[r, j];
F[r, j] = t
end
F[j, j] = s
end
end
Figure 6: LDLT factorization of an envelope-stored sparse matrix.
The only difference between Figure 4 (dense matrix) and Figure 6 (sparse envelope matrix) is that the loops do not start with the index 1 for the rows, meaning at the top of each column, but instead start at the first stored entry in each column. Clearly, Figure 6 represents a massive gain in legibility compared to the naive rewrite of the Fortran code into Julia (Figure 3), not to mention the original Fortran code.
Conclusions
Julia is a very expressive programming language, and it is appealing to consider reformulating the implementations of some the more important algorithms in older languages, such as Fortran 77 or even Fortran 90, so that they more resemble the original pseudo-code or formulas. The gain in the ability to comprehend the code in relation to the original algorithm may be well worth the effort.
References
-
Klaus-Jurgen Bathe, Finite Element Procedures in Engineering Analysis, Prentice-Hall, 1982. ISBN: 9780133173055, 0133173054 ↩



Oldest comments (7)
NIce article Petr... and the question I guess every Julia enthusiast will ask next: is the Julia Code on par or faster with the legacy Fortran one?
Thanks,
I can provide a half-way comparison, for the case of the dense matrix. The corresponding Fortran code is (in more modern notation, which is quite similar to Julia's):
You can compile it with:
Then in Julia, you can do:
And the benchmark:
The second one is the call to the fortran routine, which turns to be slightly faster. Note that I had to add
@viewsto the Julia function, otherwise the slices used in thedotoperation, by default, allocate new arrays (and the function becomes much slower).Did you use
julia -O3as well?No, but I don't see any difference in this case. (nor adding
@inboundsmakes any measurable difference for me).Good question! Yes, the two codes are the same speed (the naive rewrite into Julia and the "good" rewrite). I haven't tested the speed of the Fortran code.
Thanks for posting. These types of articles are very helpful for people who want to transition to Julia from other language systems. I like the way you have explained how Julia-specific language features can be used to implement scientific algorithms which will further help people to understand Julia code from other scientific repositories.
Add to the discussion