Julia Community 🟣

Steven Siew
Steven Siew

Posted on • Edited on

Using Riemann Zeta Function and DoubleFloats to calculate Pi

#doublefloats #mathematics

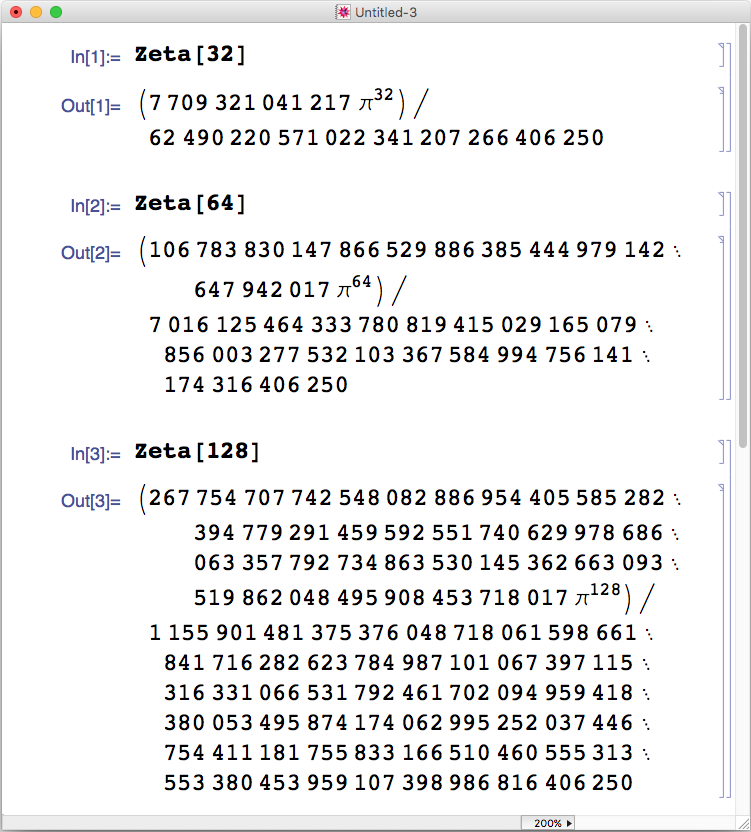
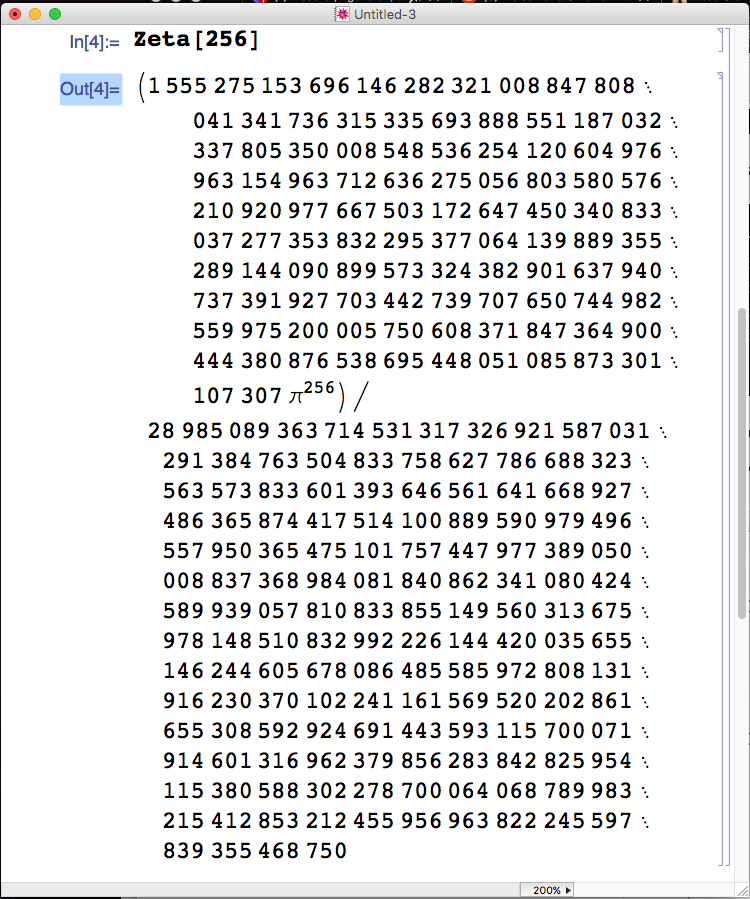
Riemann Zeta Function

Image description

It has the following particular values

Image description

DoubleFloats

DoubleFloats uses two Float64 instances to represent a single floating point number with 85 significant bits.

In this article we use it to calculate Pi because it can calculate pi to about 30 decimal digits where as normal Float64 only have 15 decimal digits.

Program 

using DoubleFloats

function calc_zeta_02(n)
    local accumulator = Double64(0)
    for k = n:-1:1
        accumulator += Double64(1)/(Double64(k)^2)
    end
    result = Double64(6) * accumulator
    result = sqrt(result)
    return result
end

function calc_zeta_04(n)
    local accumulator = Double64(0)
    for k = n:-1:1
        accumulator += Double64(1)/(Double64(k)^4)
    end
    result = Double64(90) * accumulator
    result = sqrt(sqrt(result))
    return result
end

function calc_zeta_08(n)
    local accumulator = Double64(0)
    for k = n:-1:1
        accumulator += Double64(1)/(Double64(k)^8)
    end
    result = Double64(9450) * accumulator
    result = sqrt(sqrt(sqrt(result)))
    return result
end

function calc_zeta_16(n)
    local accumulator = Double64(0)
    for k = n:-1:1
        accumulator += Double64(1)/(Double64(k)^16)
    end
    result = Double64("325641566250") / Double64(3617) * accumulator
    result = sqrt(sqrt(sqrt(sqrt(result))))
    return result
end

println("Start of program")
println("calc_zeta_02(40) = ",string(calc_zeta_02(40))  )
println("calc_zeta_04(40) = ",string(calc_zeta_04(40))  )
println("calc_zeta_08(40) = ",string(calc_zeta_08(40))  )
println("calc_zeta_16(40) = ",string(calc_zeta_16(40))  )
println("              pi = ",string(Double64(pi))     )
Enter fullscreen mode Exit fullscreen mode

It gives the following output

Start of program
calc_zeta_02(40) = 3.11792619829937803643280481368424029
calc_zeta_04(40) = 3.14158901347571579803199355470915640
calc_zeta_08(40) = 3.14159265358948106767954153673911126
calc_zeta_16(40) = 3.14159265358979323846264337322256472
              pi = 3.14159265358979323846264338327950588
Enter fullscreen mode Exit fullscreen mode

When you are adding up lots of floating point numbers, always add up the smallest number first before adding the bigger numbers. That is why we start at the highest value of k first and systematically reduce k until it reaches the value one.

Why stop at Riemann Zeta 16 when you can go even higher

When something is worth doing, it's worth overdoing.

Image description

Image description

We will just do one more to show you how powerful Riemann Zeta 32 is

function calc_zeta_32(n)
    local accumulator = Double64(0)
    for k = n:-1:1
        accumulator += Double64(1)/(Double64(k)^32)
    end
    result = Double64("62490220571022341207266406250") / Double64("7709321041217") * accumulator
    result = sqrt(sqrt(sqrt(sqrt(sqrt(result)))))
    return result
end

println("")
println("calc_zeta_16(40) = ",string(calc_zeta_16(40))  )
println("calc_zeta_32(40) = ",string(calc_zeta_32(40))  )
println("              pi = ",string(Double64(pi))     )
Enter fullscreen mode Exit fullscreen mode

with the output of


calc_zeta_16(40) = 3.14159265358979323846264337322256472
calc_zeta_32(40) = 3.14159265358979323846264338327950588
              pi = 3.14159265358979323846264338327950588
Enter fullscreen mode Exit fullscreen mode

Amazingly it only took 9 iterations to get to the same value of the constant pi in doublefloats format

julia> calc_zeta_32(9) |> string
"3.14159265358979323846264338327950588"
Enter fullscreen mode Exit fullscreen mode

Are there any alternative to writing sqrt(sqrt(sqrt(sqrt(sqrt(result)))))?

Of course there are! First we find the result of sqrt(sqrt(sqrt(sqrt(sqrt(123_456_789.0)))))

julia> sqrt(sqrt(sqrt(sqrt(sqrt(123_456_789.0)))))
1.7900280769789536
Enter fullscreen mode Exit fullscreen mode

Please notice that there are 5 sqrt in the statement above.

The solution is to create a function f such that

    #=
       func_compose(func,n)

    Compose a function multiple times
    =#
    function func_compose(func,n)
        newfunc = func
        local loop = n
        while loop > 1
            #  help?> ∘
            #  "∘" can be typed by \circ<tab>
            newfunc = func ∘ newfunc
            loop -= 1
        end
        return newfunc
    end

f = func_compose(sqrt,5)
println("f(123_456_789.0) = ",f(123_456_789.0))
Enter fullscreen mode Exit fullscreen mode

with the output

f(123_456_789.0) = 1.7900280769789536
Enter fullscreen mode Exit fullscreen mode

Note that '∘' is the Function composition operator

You don't even need to save the result of func_compose(sqrt,5) to the variable f

You can use it directly like this

julia> func_compose(sqrt,5)(123_456_789.0)
1.7900280769789536
Enter fullscreen mode Exit fullscreen mode

You can also turn func_compose() into a binary operator like this

help?> ⋏
"⋏" can be typed by \curlywedge<tab>

julia> ⋏(a,b)=func_compose(a,b)
⋏ (generic function with 1 method)

julia> (sqrt ⋏ 5)(123_456_789.0)
1.7900280769789536

julia> g = sqrt ⋏ 5
sqrt ∘ sqrt ∘ sqrt ∘ sqrt ∘ sqrt

julia> g(123_456_789.0)
1.7900280769789536
Enter fullscreen mode Exit fullscreen mode

Oldest comments (0)