Convolution in the form of a binary infix operator

#convolution #binaryoperator #mathematics

Basic introduction to Convolution

Here is a quick mathematic problem:

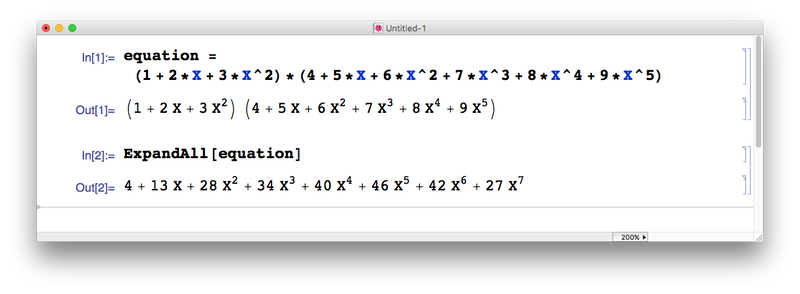
What is the result of the following polynomial multiplication?

(1 + 2*X + 3*X^2) * (4 + 5*X + 6*X^2 + 7*X^3 + 8*X^4 +9*X^5)

well the answer is (using mathematica)

4 + 13*X + 28*X^2 + 34*X^3 + 40*X^4 + 46*X^5 + 42*X^6 + 27*X^7

You can obtain the answer by using the convolution function in Julia. Unfortunately, the convolution function is NOT in base Julia but is found in the DSP.jl package

So after you have added DSP to your manifest using package manager, you can do the following.

julia> import DSP: conv

julia> conv([1,2,3],[4,5,6,7,8,9])
8-element Vector{Int64}:
  4
 13
 28
 34
 40
 46
 42
 27

You can perform the convolution as a binary infix function if you define the operator \odot as the convolution function.

# help?>  ⊙
# "⊙" can be typed by \odot<tab>

Now you can do this

julia> ⊙(x,y) = conv(x,y)
⊙ (generic function with 1 method)

julia> [1,2,3] ⊙ [4,5,6,7,8,9]
8-element Vector{Int64}:
  4
 13
 28
 34
 40
 46
 42
 27

Link to paper about convolution in Julia

https://arxiv.org/pdf/1612.08825.pdf

Link to discussion about user defined binary infix operator

3blue1brown explaination of what convolution is

Here is the link to the youtube video about convolution by 3blue1brown. He explains what a convolution really is.

How to use convolution to predict the outcome of an election for a political party

Suppose the Lion political party has three candidates (Adam,Bob and Charles) in three different electorates in an election such that

Adam has 80% chance of winning his seat
Bob has 70% chance of winning his seat
Charles has 60% chance of winning his seat

What are the chances of the Lion political party winning 0,1,2,3 seats?

julia> adam = [(1.0 - 0.8),0.8]
2-element Vector{Float64}:
 0.19999999999999996
 0.8

julia> bob = [(1.0 - 0.7),0.7]
2-element Vector{Float64}:
 0.30000000000000004
 0.7

julia> charles = [(1.0-0.6),0.6]
2-element Vector{Float64}:
 0.4
 0.6

julia> adam ⊙ bob ⊙ charles
4-element Vector{Float64}:
 0.02400000000000002
 0.18800000000000006
 0.45199999999999996
 0.33599999999999997

The answer is

2.4 % chance of winning no seats
18.8 % chance of winning only one seats
45.2 % chance of winning only two seats
33.6 % chance of winning all three seats

Using convolution to do ordinary multiplication

julia> 1234 * 5678
7006652

'''
(4 + 3 * 10^1 + 2 * 10^2 + 1 * 10^3) * (8 + 7 * 10^1 + 6 * 10^2 + 5 * 10^3)
'''

julia> result = [4,3,2,1] ⊙ [8,7,6,5]
7-element Vector{Int64}:
 32
 52
 61
 60
 34
 16
  5

julia> for k = 2:length(result)
           result[k] = result[k] + (result[k-1] ÷ 10)
           result[k-1] = result[k-1] % 10
       end

julia> result
7-element Vector{Int64}:
 2
 5
 6
 6
 0
 0
 7

julia> result = reverse(result)
7-element Vector{Int64}:
 7
 0
 0
 6
 6
 5
 2

julia> string.(result) |> join
"7006652"

You may think that it is a bit silly to use convolution to do multiplication but if you do not have access to BigInt then your only choice left is to use convolution to multiple two gigantic integers together.

Implementing convolution using Fast Fourier Transform

We can implement convolution using fast fourier transform as this article below shows

julia> result = [4,3,2,1] ⊙ [8,7,6,5]
7-element Vector{Int64}:
 32
 52
 61
 60
 34
 16
  5

# Now we do the same thing using FFT

julia> using FFTW

julia> a=Float64.([4,3,2,1])
4-element Vector{Float64}:
 4.0
 3.0
 2.0
 1.0

julia> b=Float64.([8,7,6,5])
4-element Vector{Float64}:
 8.0
 7.0
 6.0
 5.0

julia> len_final = length(a) + length(b) - 1
7

julia> extra_padding_for_a = len_final - length(a)
3

# Pad a with some extra paddings of zeros
julia> aa = vcat(a,[0,0,0])
7-element Vector{Float64}:
 4.0
 3.0
 2.0
 1.0
 0.0
 0.0
 0.0

julia> extra_padding_for_b = len_final - length(b)
3

# Pad b with some extra paddings of zeros
julia> bb = vcat(b,[0,0,0])
7-element Vector{Float64}:
 8.0
 7.0
 6.0
 5.0
 0.0
 0.0
 0.0

julia> a_fft = fft(aa)
7-element Vector{ComplexF64}:
               10.0 + 0.0im
  4.524458669761152 - 4.729234010885294im
 2.1539892641849523 - 1.275184775842325im
 2.3215520660538953 - 0.7129161645984384im
 2.3215520660538953 + 0.7129161645984384im
 2.1539892641849523 + 1.275184775842325im
  4.524458669761152 + 4.729234010885294im

julia> b_fft = fft(bb)
7-element Vector{ComplexF64}:
              26.0 + 0.0im
 6.524458669761152 - 13.491806545954942im
 4.153989264184952 - 0.31203553822726793im
 4.321552066053895 - 3.2208368399238467im
 4.321552066053895 + 3.2208368399238467im
 4.153989264184952 + 0.31203553822726793im
 6.524458669761152 + 13.491806545954942im

julia> product_fft = a_fft .* b_fft
7-element Vector{ComplexF64}:
             260.0 + 0.0im
 -34.2862667915158 - 91.89881294123597im
  8.54974531072476 - 5.969225068086821im
 7.736521480791037 - 10.558244744191306im
 7.736521480791037 + 10.558244744191306im
  8.54974531072476 + 5.969225068086821im
 -34.2862667915158 + 91.89881294123597im

julia> ff = ifft(product_fft)
7-element Vector{ComplexF64}:
              32.0 + 0.0im
              52.0 + 0.0im
              61.0 + 0.0im
 60.00000000000001 + 0.0im
 34.00000000000001 + 0.0im
              16.0 + 0.0im
               5.0 + 0.0im

julia> final_result = real.(ff)
7-element Vector{Float64}:
 32.0
 52.0
 61.0
 60.00000000000001
 34.00000000000001
 16.0
  5.0

# compare with
julia> result = [4,3,2,1] ⊙ [8,7,6,5]
7-element Vector{Int64}:
 32
 52
 61
 60
 34
 16
  5

Now put them together to perform integer multiplication using FFT

function fft_multiplication(str_a,str_b)
    local arr_a, arr_b, len_final
    local extra_padding_for_a
    arr_a = Float64.( reverse(map(x->parse(Int64,x),split(str_a,""))) )
    arr_b = Float64.( reverse(map(x->parse(Int64,x),split(str_b,""))) )
    len_final = length(arr_a) + length(arr_b) - 1
    extra_padding_for_a = len_final - length(arr_a)
    extra_padding_for_b = len_final - length(arr_b)
    arr_a = vcat(arr_a,[ 0.0 for k in 1:extra_padding_for_a ])
    arr_b = vcat(arr_b,[ 0.0 for k in 1:extra_padding_for_b ])
    local a_fft = fft(arr_a)
    local b_fft = fft(arr_b)
    local product_fft = a_fft .* b_fft
    local complex_temp = ifft(product_fft)
    local result = real.(complex_temp)
    result = Int64.(  map(x->round(x,RoundNearest),result)  )
    local k
    for k = 2:length(result)
           result[k] = result[k] + (result[k-1] ÷ 10)
           result[k-1] = result[k-1] % 10
    end
    result = reverse(result)
    result = join(string.(result))
    return result
end

julia> println( fft_multiplication("12345","67890")  )
838102050

# compare with
julia> 12345 * 67890
838102050

Finally the algorithm for a very naive implementation of convolution

How can we talk about convolution without a naive implementation of convolution. This is a very inefficient implementation of an algorithm to calculate convolution.

function naive_convolution(data, kernel)
    local len_data = length(data)
    local len_kernel = length(kernel)
    local len_ans = len_data + len_kernel - 1
    local typeofdata = eltype(data)
    local ans = zeros(typeofdata, len_ans)
    local j,k,acc,loc

    # Next we work out the value for each of the element of the solution
    for j = 1:len_ans
        acc = zero(typeofdata)
        for k = 1:len_kernel
            loc = j - (k - 1)
            if !( loc < 1 || loc > len_data )
                acc += data[loc] * kernel[k]
            end
        end
        ans[j] = acc
    end
    return ans
end