Finding the location of Cerberus
HMVS Cerberus is a warship that was "sunk" in blackrock. You can see the ship from shore. The objective is to find the location of HMS Cerberus without a boat.
You can measure the bearing to the ship from two locations
- Shore : bearing to ship is 263.3 degrees
- Pier : bearing to ship is 305.8 degrees
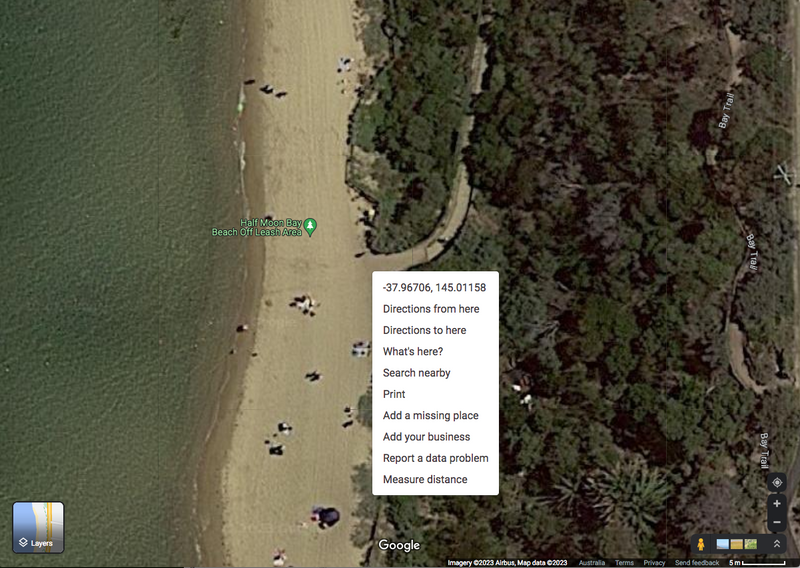
Using Google maps, you can get the location of the two shore locations. To get the location, right click on the spot you are interested in.
- Shore : location is -37.96705678343727 (latitude), 145.01158473574677 (longtitude)
- Pier : location is -37.968305948144405 (latitude), 145.00959897290315 (longtitude)
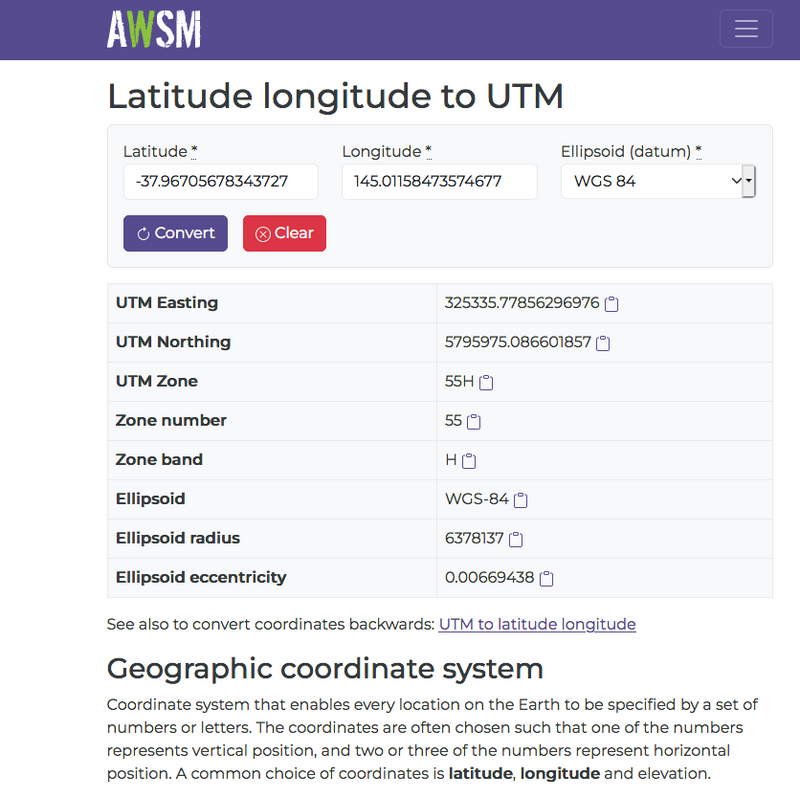
To get the location into an XY coordinate system, we use this website and set the earth geographic datum as WGS84.
https://awsm-tools.com/lat-long-to-utm?form%5Bellipsoid%5D=WGS+84
This gives us the WGS84 GPS coordinates system where the numbers are in units of meters/metres. The three numbers are
- UTM ZONE (eg. 55H which is zone number 55 with Latitude Band H)
- Easting (number of meters east from a virtual base location)
- Northing (number of meters north from a virtual base location)
You can read more about the UTM coordinate system below
https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system
Our details are
- Shore : location is 325335.77856296976 (E) 5795975.086601857 (N) 55H (UTM Zone)
- Pier : location is 325164.2938595414 (E) 5795832.741503723 (N) 55H (UTM Zone)
Now that we got all the information that we needed, we can calculate the location of the Cerebus/target
Julia source code to calculate location
First we give you the entire source code in Julia so that you can copy and paste it into a textfile.
This source code requires the following packages
- Printf
- Measurements
using Printf
#= Crosspoint_print(x)
Print coordinates to two decimal places
=#
function Crosspoint_print(x)
if length(x) == 1
print(rstrip(@sprintf("%-10.2f", x)))
return
end
local flag = false
print("[")
for ele in x
print(flag==true ? "," : "")
print(rstrip(@sprintf("%-10.2f", ele)))
flag = true
end
print("]")
end
Crosspoint_println(x) = begin Crosspoint_print(x); println(); end
#= intersect2lines(A,a,B,b)
Return the intersection of two lines from
two known points A,B using sin_degree() and
cos_degree() only. a and b are the bearings
from the unknown position to the two known points A,B
=#
function intersect2lines(A,a,B,b)
den = sind(a - b) # sind() function is Sine in degrees, cosd() is similar
tempX = B[1]*cosd(b)*sind(a) - (A[1]*cosd(a) + (B[2] - A[2])*sind(a))*sind(b)
tempY = A[2]*cosd(b)*sind(a) - cosd(a)*((A[1] - B[1])*cosd(b) + B[2]*sind(b))
newX = tempX/den
newY = tempY/den
return [newX,newY]
end
#= triangulation(A,a,B,b)
Return the position of an unknown location
by triagulation from two known points A,B and
the bearing from those two known points A,B to
the unknown location
=#
triangulation(A,a,B,b) = intersect2lines(A,a+180.0,B,b+180.0)
Pos_Shore = (325335.78,5795975.09) # Easting 325335.78 Northing 5795975.09
Pos_Shore_bearing_to_target = 263.3 # 263.3 degrees
Pos_Pier = (325164.29,5795832.74) # Easting 325164.29 Northing 5795832.74
Pos_Pier_bearing_to_target = 305.8 # 305.8 degrees
println("program start")
println("The coordinates for :")
print("Shore is ")
Crosspoint_println(Pos_Shore)
print("Pier is ")
Crosspoint_println(Pos_Pier)
println("")
println("Bearing from shore to cerberus/target is ",round(Pos_Shore_bearing_to_target,digits=1))
println("Bearing from pier to cerberus/target is ",round(Pos_Pier_bearing_to_target,digits=1))
println("")
target_pos_estimate = triangulation(Pos_Shore,
Pos_Shore_bearing_to_target,
Pos_Pier,
Pos_Pier_bearing_to_target)
print("The estimated position of target is ")
Crosspoint_println(target_pos_estimate)
println("In coordinate format of [Easting value,Northing value]")
println("")
println("Now we do the same thing again using measurement")
println("")
#
# Now use Measurement to measure the uncertainties
# help?> ±
# "±" can be typed by \pm<tab>
using Measurements
Shore = (325335.78 ± 5.0,5795975.09 ± 5.0)
Pier = (325164.29 ± 5.0,5795832.74 ± 5.0)
Shore_bearing_to_target = 263.3 ± 0.5
Pier_bearing_to_target = 305.8 ± 0.5
target_pos_estimate2 = triangulation(Shore,
Shore_bearing_to_target,
Pier,
Pier_bearing_to_target)
value_two_decimal_places(m) = rstrip( @sprintf("%-16.2f",Measurements.value(m)) )
uncertainty_two_decimal_places(m) = rstrip( @sprintf("%-16.2f",Measurements.uncertainty(m)) )
print("The estimated position of target using Measurements package is ")
print("[")
print(value_two_decimal_places(target_pos_estimate2[1]))
print(" ± ")
print(uncertainty_two_decimal_places(target_pos_estimate2[1]))
print(",")
print(value_two_decimal_places(target_pos_estimate2[2]))
print(" ± ")
print(uncertainty_two_decimal_places(target_pos_estimate2[2]))
println("]")
println("")
dict_uncertainty_in_easting = Measurements.uncertainty_components(target_pos_estimate2[1])
dict_uncertainty_in_northing = Measurements.uncertainty_components(target_pos_estimate2[2])
println("Uncertainty in the easting value")
for key in keys(dict_uncertainty_in_easting)
println(key," => ",dict_uncertainty_in_easting[key])
end
println("")
println("Uncertainty in the northing value")
for key in keys(dict_uncertainty_in_northing)
println(key," => ",dict_uncertainty_in_northing[key])
end
Now we display the screen output of the program
program start
The coordinates for :
Shore is [325335.78,5795975.09]
Pier is [325164.29,5795832.74]
Bearing from shore to cerebus/target is 263.3
Bearing from pier to cerebus/target is 305.8
The estimated position of target is [325018.58,5795937.83]
In coordinate format of [Easting value,Northing value]
Now we do the same thing again using measurement
The estimated position of target using Measurements
package is [325018.58 ± 10.32,5795937.83 ± 5.04]
Uncertainty in the easting value
(5.79583274e6, 5.0, 0x0000000000000004) => 5.961637475221173
(263.3, 0.5, 0x0000000000000005) => 3.345995971168122
(305.8, 0.5, 0x0000000000000006) => 2.304707563592274
(5.79597509e6, 5.0, 0x0000000000000002) => 5.961637475221173
(325164.29, 5.0, 0x0000000000000003) => 4.299668552553106
(325335.78, 5.0, 0x0000000000000001) => 0.7003314474468948
Uncertainty in the northing value
(5.79583274e6, 5.0, 0x0000000000000004) => 0.7003314474468948
(263.3, 0.5, 0x0000000000000005) => 2.4132084035663866
(5.79597509e6, 5.0, 0x0000000000000002) => 4.299668552553106
(305.8, 0.5, 0x0000000000000006) => 0.27074091483518714
(325335.78, 5.0, 0x0000000000000001) => 0.5050949698748158
(325164.29, 5.0, 0x0000000000000003) => 0.5050949698748158
julia>
Next we will talk about each section of the Julia program to explain how it is accomplished.
Crosspoint_print()
Now we will talk about the function Crosspoint_print() and Crosspoingg_println()
using Printf
#= Crosspoint_print(x)
Print coordinates to two decimal places
=#
function Crosspoint_print(x)
if length(x) == 1
print(rstrip(@sprintf("%-10.2f", x)))
return
end
local flag = false
print("[")
for ele in x
print(flag==true ? "," : "")
print(rstrip(@sprintf("%-10.2f", ele)))
flag = true
end
print("]")
end
Crosspoint_println(x) = begin Crosspoint_print(x); println(); end
Crosspoint_print() will printout a floating point number (or a tuple or an array of floating point number) to two decimal places.
For example:
julia> Crosspoint_print(pi)
3.14
julia> Crosspoint_print([pi,2*pi])
[3.14,6.28]
julia> Crosspoint_print([pi,2*pi,pi^2])
[3.14,6.28,9.87]
julia> Crosspoint_print((pi,2*pi,pi^2))
[3.14,6.28,9.87]
The purposes of Crosspoint_print() is to easily print out the coordinates. For example:
julia> Pos_Shore = (325335.78,5795975.09)
(325335.78, 5.79597509e6)
julia> print( Pos_Shore )
(325335.78, 5.79597509e6)
julia> Crosspoint_print( Pos_Shore )
[325335.78,5795975.09]
intersect2lines() and triangulation()
Now we will talk about the function intersect2lines() and triangulation()
#= intersect2lines(A,a,B,b)
Return the intersection of two lines from
two known points A,B using sin_degree() and
cos_degree() only. a and b are the bearings
from the unknown position to the two known points A,B
=#
function intersect2lines(A,a,B,b)
den = sind(a - b) # sind() function is Sine in degrees, cosd() is similar
tempX = B[1]*cosd(b)*sind(a) - (A[1]*cosd(a) + (B[2] - A[2])*sind(a))*sind(b)
tempY = A[2]*cosd(b)*sind(a) - cosd(a)*((A[1] - B[1])*cosd(b) + B[2]*sind(b))
newX = tempX/den
newY = tempY/den
return [newX,newY]
end
#= triangulation(A,a,B,b)
Return the position of an unknown location
by triagulation from two known points A,B and
the bearing from those two known points A,B to
the unknown location
=#
triangulation(A,a,B,b) = intersect2lines(A,a+180.0,B,b+180.0)
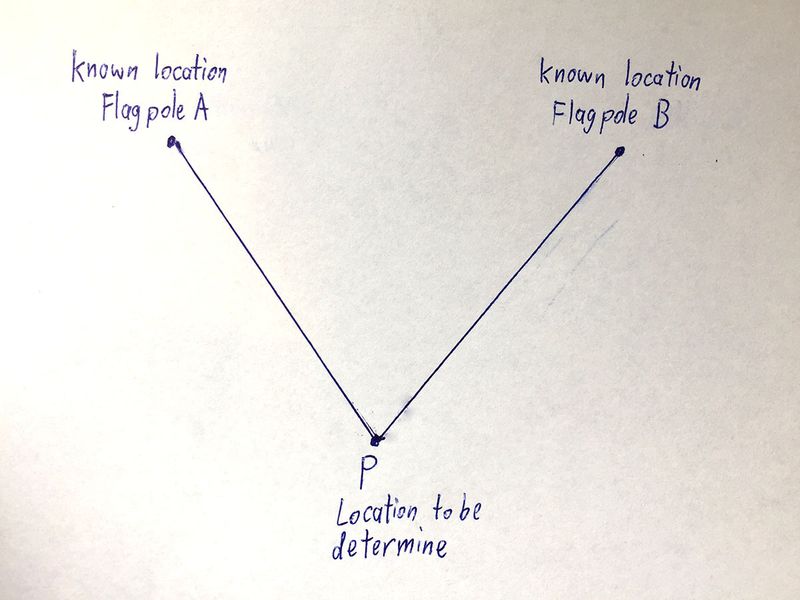
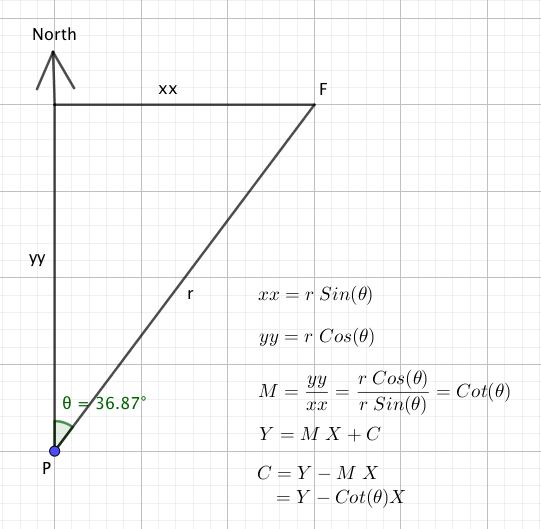
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from two (or more) known points.
So the question is "How do we develop triangulation?"
We start from FIRST PRINCIPLES
Next we assume we knew the equation of the line (aka Y = M * X + C ) and work out the location of the unknown location.
Now to find the value of X and Y, both X & Y at point P , all we have to do is to find the values of
- M1
- C1
- M2
- C2
So now we know that
- M1 = Cot(bearing to flagpole A)
- M2 = Cot(bearing to flagpole B)
- C1 = Y_flagpoleA - Cot(bearing to flagpole A) * X_flagpoleA
- C2 = Y_flagpoleB - Cot(bearing to flagpole B) * X_flagpoleB
Next we put together everything that we know
The value for X is
The value for Y is
And so in SUMMARY, the location of unknown location is
Which is what is in our function intersect2lines(A,a,B,b)
function intersect2lines(A,a,B,b)
den = sind(a - b) # sind() function is Sine in degrees, cosd() is similar
tempX = B[1]*cosd(b)*sind(a) - (A[1]*cosd(a) + (B[2] - A[2])*sind(a))*sind(b)
tempY = A[2]*cosd(b)*sind(a) - cosd(a)*((A[1] - B[1])*cosd(b) + B[2]*sind(b))
newX = tempX/den
newY = tempY/den
return [newX,newY]
end
Regarding the function triangulation()
The difference between intersect2lines() and triangulation() is very simple.
The function intersect2lines() assumes that you are in location P and you have the following two bearings:
- bearing a from location P to Flagpole A
- bearing b from location P to Flagpole B
Whereas the function triangulation() assumes that you are
at the two Flagpoles and you have the following two bearings:
- bearing a from Flagpole A to location P
- bearing b from Flagpole B to location P
So you see the only difference is 180 degrees so
triangulation(A,a,B,b) = intersect2lines(A,a+180.0,B,b+180.0)
Location of Cerberus
So with the Julia code
target_pos_estimate = triangulation(Pos_Shore,
Pos_Shore_bearing_to_target,
Pos_Pier,
Pos_Pier_bearing_to_target)
print("The estimated position of target is ")
Crosspoint_println(target_pos_estimate)
println("In coordinate format of [Easting value,Northing value]")
We can now get the location of the Cerberus
The estimated position of target is [325018.58,5795937.83]
In coordinate format of [Easting value,Northing value]
Once you got the location of Cerberus in UTM format, you can convert it back to Latitude and Longitude using this website
https://awsm-tools.com/utm-to-lat-long
Now we do the same thing again but this time with Measurements
Measurements is a Julia package that allows us to include (the amount of) uncertainties in our input values.
To input uncertainties, we type '\' , 'p' , 'm' , <TAB> on the REPL or a Julia Editor.
#
# Now use Measurement to measure the uncertainties
# help?> ±
# "±" can be typed by \pm<tab>
using Measurements
Shore = (325335.78 ± 5.0,5795975.09 ± 5.0)
Pier = (325164.29 ± 5.0,5795832.74 ± 5.0)
Shore_bearing_to_target = 263.3 ± 0.5
Pier_bearing_to_target = 305.8 ± 0.5
For example: Shore_bearing_to_target = 263.3 ± 0.5
The variable "Shore_bearing_to_target" is a measurement.
The measurement "Shore_bearing_to_target" has two components.
- The first component is called "value"
- The second component is called "uncertainty"
This function returns the "value" of a measurement
- Measurements.value()
This other function returns the "uncertainty" of a measurement
- Measurements.uncertainty()
I have the following two functions to return the numeric value of the two above components in a string
value_two_decimal_places(m) = rstrip( @sprintf("%-16.2f",Measurements.value(m)) )
uncertainty_two_decimal_places(m) = rstrip( @sprintf("%-16.2f",Measurements.uncertainty(m)) )
The location with uncertainties
So here is the location with uncertainties
target_pos_estimate2 = triangulation(Shore,
Shore_bearing_to_target,
Pier,
Pier_bearing_to_target)
print("The estimated position of target using Measurements package is ")
print("[")
print(value_two_decimal_places(target_pos_estimate2[1]))
print(" ± ")
print(uncertainty_two_decimal_places(target_pos_estimate2[1]))
print(",")
print(value_two_decimal_places(target_pos_estimate2[2]))
print(" ± ")
print(uncertainty_two_decimal_places(target_pos_estimate2[2]))
println("]")
println("")
Here is the output
Now we do the same thing again using measurement
The estimated position of target using Measurements
package is [325018.58 ± 10.32,5795937.83 ± 5.04]
Relative contributions to the uncertainties
dict_uncertainty_in_easting = Measurements.uncertainty_components(target_pos_estimate2[1])
dict_uncertainty_in_northing = Measurements.uncertainty_components(target_pos_estimate2[2])
println("Uncertainty in the easting value")
for key in keys(dict_uncertainty_in_easting)
println(key," => ",dict_uncertainty_in_easting[key])
end
println("")
println("Uncertainty in the northing value")
for key in keys(dict_uncertainty_in_northing)
println(key," => ",dict_uncertainty_in_northing[key])
end
Consider the uncertainties for the "northing" of Cerberus
5795937.83 ± 5.04
The uncertainty for the northing is 5.04 but where does it comes from?
It came from the following input measurements
- Shore Easting
- Shore Northing
- Shore_bearing_to_target
- Pier Easting
- Pier Northing
- Pier_bearing_to_target
There is a way to determine the "relative" contribution to the final uncertainty.
Uncertainty in the northing value
(5.79583274e6, 5.0, 0x0000000000000004) => 0.7003314474468948
(263.3, 0.5, 0x0000000000000005) => 2.4132084035663866
(5.79597509e6, 5.0, 0x0000000000000002) => 4.299668552553106
(305.8, 0.5, 0x0000000000000006) => 0.27074091483518714
(325335.78, 5.0, 0x0000000000000001) => 0.5050949698748158
(325164.29, 5.0, 0x0000000000000003) => 0.5050949698748158
Here we see that the value 5795975.09 (Which is Shore Northing) contributes 4.29966 of relative weight to the final uncertainty of the northing value of Cerberus and this INPUT parameter is THE BIGGEST contribution.
This means that if you reduce the uncertainty for Shore Northing, you will get the biggest bang per buck for lowering the final uncertainty for "northing" of the Cerberus.
This mean that if you want to get the biggest bang per buck for lowering the final uncertainty for "northing" of the Cerberus, you should put all your effort into reducing the uncertainty for Shore Northing.



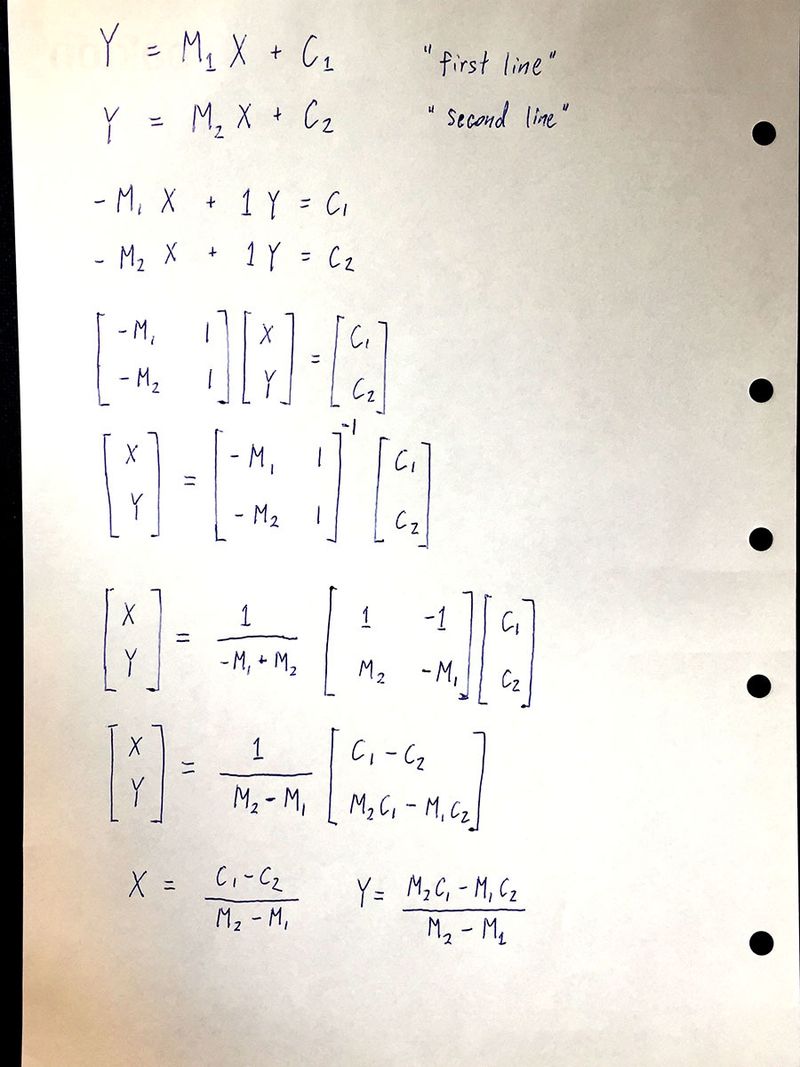




Latest comments (2)
As a complete novice on this topic I would like to know how you measure the bearing to the ship from the two locations?
With a compass. You stand at the location, look towards the Target and then read the direction on the compass. The direction on your compass is the bearing from your current location to the Target. Watch the Youtube Video youtu.be/-Ak86suJFjo
postscript: do not forget to correct for magnetic declination