Introduction
At the risk of going full recipe blog, I'm going to start with a boring but harmless personal anecdote.
When I was a wee lad, I thought that the secret to fame and fortune was solving Project Euler problems. If you aren't familiar, they describe it as,
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems.
It would still be a couple years before I discovered Julia, but armed with my rudimentary understanding of CALC101 and even more rudimentary understanding of Python 2.7, I got to work. I'm neither famous nor rich so the obvious conclusion is that I didn't solve enough problems, but I hacked my way through a few. Eventually it became clear that I simply didn't have the algorithmic chops (or patience) to make much more headway so I transitioned from solving problems to just sort of skimming them and seeing if I could think of anything in five minutes. You might be surprised to learn that this actually worked for one (1) problem.
I stumbled onto Problem 317: Firecracker. There were no gigantic prime numbers or arrays of obtusely defined integers, it was just good old projectile motion.
A firecracker explodes at a height of above level ground. It breaks into a large number of very small fragments, which move in every direction; all of them have the same initial velocity of .
We assume that the fragments move without air resistance, in a uniform gravitational field with .
Find the volume (in ) of the region through which the fragments move before reaching the ground. Give your answer rounded to four decimal places.
This problem will be today's topic. I'll show you the solution I came up with all those years ago, and atone for my past sins by also providing a Julia solution. For complete transparency, reading further will spoil the problem!
The Codeless Solution
First, clearly we need some physics - without knowing how a projectile behaves this problem is simply impossible (e.g. what if it had air drag?) A quick skim of the first chapter of any physics textbook will tell us the height of the firecracker
as a function of its horizontal displacement
is given by
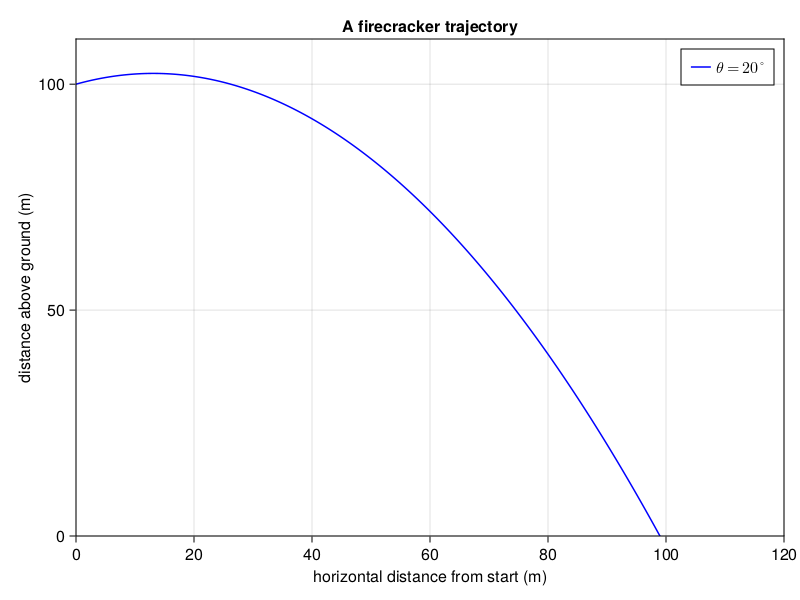
where is the initial height, is the initial velocity, is the acceleration due to gravity and is the launch angle with respect to the horizontal. Let's get plotting; we'll assume that the firecracker is launched to the "right" and only look at the part of the trajectory above . I realize that the title of this section is "codeless solution" and I'm about to show some code, but that's showbiz baby.
using Makie, CairoMakie
const y0 = 100.0
const v = 20.0
const g = 9.81
# keep θ in degrees
y(x; θ) = y0 + x*tan(π*θ/180) - g*sec(π*θ/180)^2*x^2/(2*v^2)
xs = range(0.0, 120.0, step = 0.1)
ys = map(x -> y(x, θ = 20), xs)
fig = Figure()
ax = Axis(
fig[1,1],
limits = (0, 120, 0, 110),
title = "A firecracker trajectory",
xlabel = "horizontal distance from start (m)",
ylabel = "distance above ground (m)"
)
lines!(ax, xs, ys, color = :blue, label = L"\theta = 20^\circ")
axislegend(ax)
fig
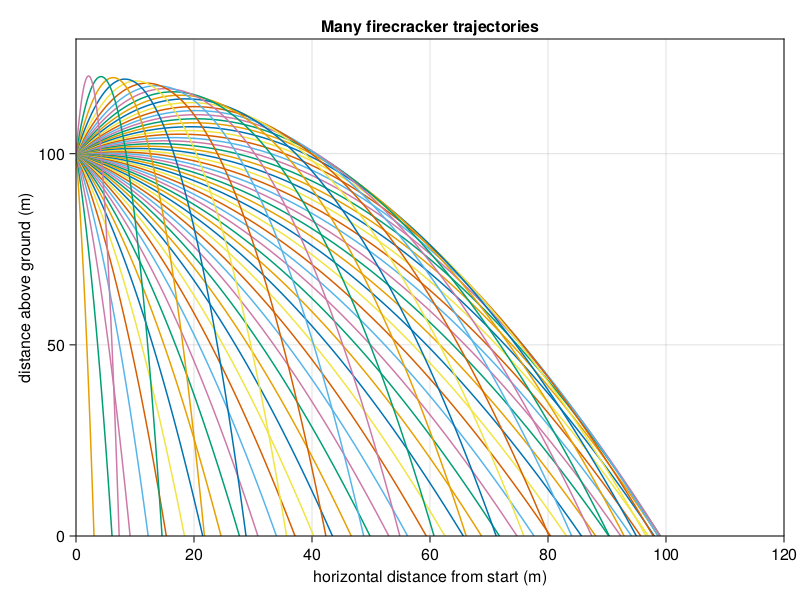
We see a parabola, which is reassuring. But what's all this about "volume" of the region the projectile moves through? The question advises us that "It breaks into a large number of very small fragments, which move in every direction...", so let's try plotting many trajectories for various launch angles.
fig = Figure()
ax = Axis(
fig[1,1],
limits = (0, 120, 0, 130),
title = "Many firecracker trajectories",
xlabel = "horizontal distance from start (m)",
ylabel = "distance above ground (m)"
)
for θ in range(-90.0, 90.0, step = 3.0)
xs = range(0.0, 120.0, step = 0.1)
ys = map(x -> y(x, θ = θ), xs)
lines!(ax, xs, ys)
end
fig
Now the game is clear: the continuum of trajectories traces out a shape, so what we really need is somehow the "boundary" of all of these individual trajectories. If we knew that, we could determine the area traced out by all the trajectories, which is one step closer to the volume. But how to obtain such a thing?
To answer this, we have to think about what exactly is meant by "boundary" of the trajectories. Well, it's certainly some kind of function . But, given some , what is the value of ? If we examine the figure, the "boundary" of the trajectories at a given looks like the largest value attained by for any . But that's exactly it:
So for a given
, we just need to compute the maximum of
, treating it then as a function of
. This is accomplished by routine calculus,
Substituting this into gives our boundary as
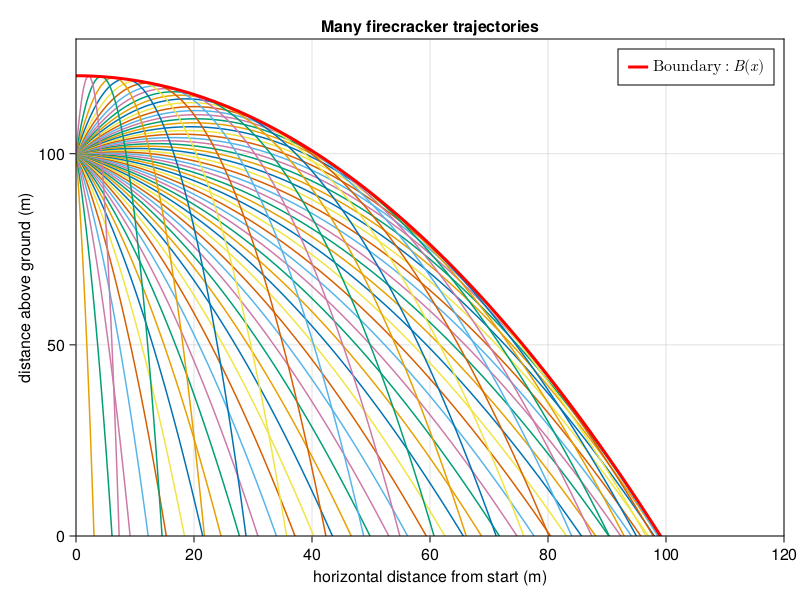
So (fascinatingly, in my opinion) the boundary of a set of parabolic trajectories is itself a parabola! The boundary is more usually called the envelope and is obtained for a parametric function by simply extremizing the parameter in question (in our case, ) but I certainly didn't know that back in the day.
A neat observation: the quantity
is actually the height attained by a projectile shot straight up in the air. Therefore, setting
actually allows us to write
Anyway, let's check out
on our plot.
const ymax = v^2/(2*g)
B(x) = y0 + ymax*(1 - x^2/(4*ymax^2))
xs = range(0.0, 120.0, step = 0.1)
ys = B.(xs)
lines!(ax, xs, ys,
linewidth = 3.0,
color = :red,
label = L"\mathrm{Boundary: } B(x)")
axislegend(ax)
fig
Well there it is. So the area swept out by the trajectories is the area between the
axis and the function
. But how to get the volume? This is, to date, the absolute only single time I have used a volume of revolution calculation. You may have realized that the calculations we've done so far only hold for a "slice" of the volume. After all, the firecrackers are being ejected in all directions in space. But then, since each direction looks the same as any other, we can get the total volume from the area under
by revolving
around the
axis using the method of cylinders. In brief, this simply states that the volume of a little chunk of cylinder is its circumference
times its height
times its width
. Noting that
, we therefore integrate
a very slick result indeed. We can then obtain the final answer:
2*π*(1 + y0/ymax)^2 * ymax^3
1.8565328455275737e6
The Julia Solution
To solve the problem in a "code-y" way, we'll essentially perform the above calculation, but numerically. First, we'll get
by solving the optimization problem using Optim.jl. Then, we can integrate the result using QuadGK.jl.
using Optim
using QuadGK
boundary(x) = -1*optimize(θ -> -y(x, θ = θ), 0.0, 90.0).minimum
@time quadgk(x -> 2*π*x*boundary(x), 0, 2*ymax*sqrt(1 + y0/ymax))[1]
0.314286 seconds (286.15 k allocations: 16.542 MiB, 5.87% gc time, 99.95% compilation time)
1.8565328455275744e6
It's just that easy folks.
Conclusion
Even though this problem doesn't end up being that hard, it's been living in my head more or less rent-free for over ten years so it's nice to finally write it down. My Project Euler career has been over for a long time, but there's still some good stuff in there. Let me know if solving them gets you rich and famous.


Top comments (2)
how come you're neither famous nor rich :exploiding_head
great post!
Thank you!!