Julia Community 🟣

Cover image for Frequentist and Bayesian coin flipping in Julia
Rik Huijzer
Rik Huijzer

Posted on • Edited on • Originally published at huijzer.xyz

Frequentist and Bayesian coin flipping in Julia

#bayesian #statistics

To me, it is still unclear what exactly is the difference between Frequentist and Bayesian statistics. Most explanations involve terms such as "likelihood", "uncertainty" and "prior probabilities". Here, I'm going to show the difference between both statistical paradigms by using a coin flipping example. In the examples, the effect of showing more data to both paradigms will be visualised.

Generating data

Lets start by generating some data from a fair coin flip, that is, the probability of heads is 0.5.

begin
    import CairoMakie

    using AlgebraOfGraphics: Lines, Scatter, data, draw, visual, mapping
    using Distributions
    using HypothesisTests: OneSampleTTest, confint
    using StableRNGs: StableRNG
end
Enter fullscreen mode Exit fullscreen mode 
n = 80;
Enter fullscreen mode Exit fullscreen mode 
p_true = 0.5;
Enter fullscreen mode Exit fullscreen mode 
is_heads = let
    rng = StableRNG(15)
    rand(rng, Bernoulli(p_true), n);
end;
Enter fullscreen mode Exit fullscreen mode

To give some intuition about the sample, the first six elements of is_heads are:

is_heads[1:6]
Enter fullscreen mode Exit fullscreen mode 
6-element Vector{Bool}:
 1
 1
 1
 0
 0
 1
Enter fullscreen mode Exit fullscreen mode

Calculate probability estimates

The Frequentist estimate for a one sample t-test after seeing nnn samples can be calculated with

function frequentist_estimate(n)
    t_result = OneSampleTTest(is_heads[1:n])
    middle = t_result.xbar
    lower, upper = confint(t_result)
    return (; lower, middle, upper)
end;
Enter fullscreen mode Exit fullscreen mode

For the Bayesian estimate, we can use the closed-form solution (https://turing.ml/dev/tutorials/00-introduction/). A closed-form solution is not available for many real-world problems, but quite useful for this example.

closed_form_prior = Beta(1, 1);
Enter fullscreen mode Exit fullscreen mode 
function update_belief(k)
    heads = sum(is_heads[1:k-1])
    tails = k - heads
    updated_belief = Beta(closed_form_prior.α + heads, closed_form_prior.β + tails)
    return updated_belief
end;
Enter fullscreen mode Exit fullscreen mode 
beliefs = [closed_form_prior; update_belief.(1:n)];
Enter fullscreen mode Exit fullscreen mode 
function bayesian_estimate(n)
    distribution = beliefs[n]
    q(x) = quantile(distribution, x)
    lower = q(0.025)
    middle = mean(distribution)
    upper = q(0.975)
    return (; lower, middle, upper)
end;
Enter fullscreen mode Exit fullscreen mode

Now we can write a function to plot the estimates:

function plot_estimates(estimate_function; title="")
    draws = 2:4:80
    estimates = estimate_function.(draws)
    middles = [t.middle for t in estimates]
    lowers = [t.lower for t in estimates]
    uppers = [t.upper for t in estimates]
    df = (; draws, estimates, P=middles)
    layers = data(df) * visual(Scatter)
    df_middle = (; P=fill(0.5, length(draws) + 2), draws=[-1; draws; 83])
    layers += data(df_middle) * visual(Lines) * visual(linestyle=:dash)
    for (n, lower, upper) in zip(draws, lowers, uppers)
        df_bounds = (; P=[lower, upper], draws=[n, n])
        layers += data(df_bounds) * visual(Lines)
    end

    axis = (; yticks=0:20:80, limits=((-0.2, 1.2), nothing), title)
    map = mapping(:P => "Probability of heads", :draws => "Observed number of draws")
    draw(layers * map; axis)
end;
Enter fullscreen mode Exit fullscreen mode

And plot the Frequentist and Bayesian estimates:

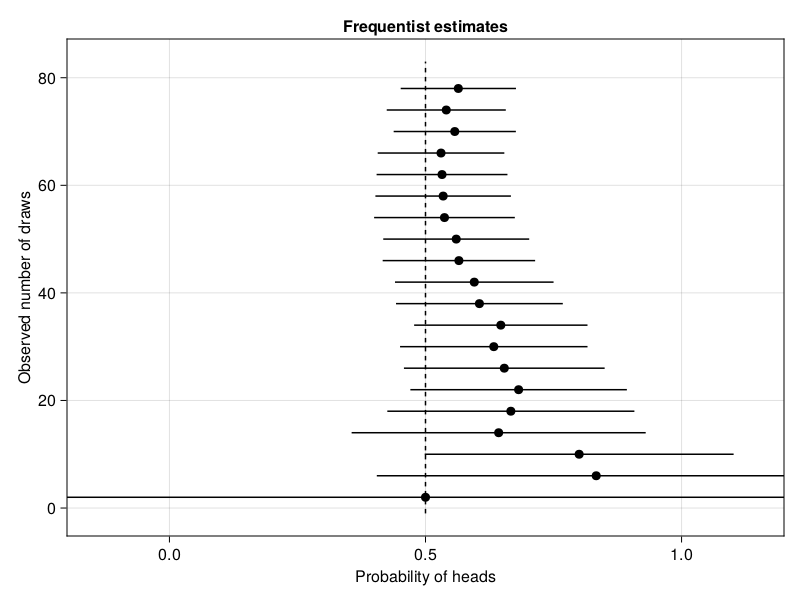
plot_estimates(frequentist_estimate; title="Frequentist estimates")
Enter fullscreen mode Exit fullscreen mode

Frequentist estimate

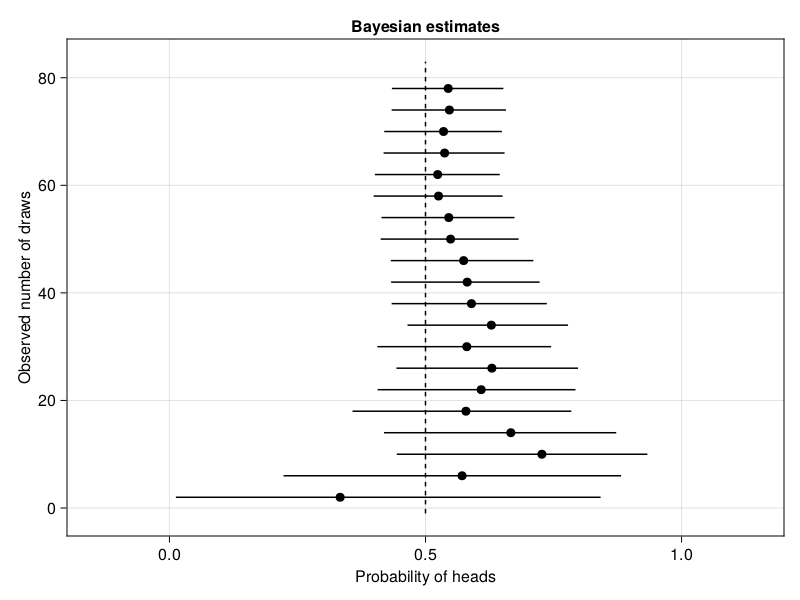
plot_estimates(bayesian_estimate; title="Bayesian estimates")
Enter fullscreen mode Exit fullscreen mode

Bayesian estimate

Conclusion

Based on these plots, we can conclude two things. Firstly, the Bayesian approach provides better estimates for small sample sizes. The Bayesian approach successfully uses the fact that a probability should be between 0 and 1, which was given to the model via the Beta(1, 1) prior. For increasingly larger sample sizes, the difference between both statistical paradigms vanish in this situation. Secondly, collecting more and more samples until the result is significant is dangerous. This approach is called optional stopping. Around 10 samples, the frequentist' test would conclude that the data must come from a distribution with a mean higher than 0.5, whereas we know that this is false. Cumming (2011) calls this the "dance of the p-values".

EDIT: Christopher Rowley pointed out that it would be more fair to run a frequentist BinomialTest since that will output a confidence interval in [0, 1].

Built with Julia 1.8.0 and

AlgebraOfGraphics 0.6.11
CairoMakie 0.8.13
Distributions 0.25.70
HypothesisTests 0.10.10
StableRNGs 1.0.0
Enter fullscreen mode Exit fullscreen mode

To run this blog post locally, open this notebook with Pluto.jl.

Top comments (5)

Collapse
 
cjdoris profile image
Christopher Rowley •

Nice article. Just one thing, since you are estimating a probability, a BinomialTest is more appropriate than a OneSampleTTest. This will output a confidence interval in [0,1] and be more accurate, especially at lower numbers of samples. This addresses the first part of your conclusion.

Collapse
 
rikhuijzer profile image
Rik Huijzer •

Thank you. I didn't know that and added a comment in the article.

Collapse
 
getzdan profile image
getzdan • • Edited

Lovely article, and I'm just reading up on these topics. My question is regarding the Conclusion section, it says "around 30 samples..." and looking at the frequentist plot, I can see 0.5 being firmly within the confidence interval the whole process. Am I missing something? Did the comment refer to a different random seed?
(also, it seems Turing.jl isn't used, so it doesn't have to be imported. The Bayesian calculation is similar to one in Turing documentation on the section of calculation without Turing).

Collapse
 
rikhuijzer profile image
Rik Huijzer •

Thank you! You are right.

I've switched from loading Turing.jl to only Distributions.jl. Regarding the confidence interval, I was using a Random.seed! instead of the StableRNG, so that broke things when I updated this post to Julia 1.8. It's fixed now.

Collapse
 
davibarreira profile image
Davi Sales Barreira • • Edited

Very nice article. The difference is in terms of interpretation, but can be meaningful in the way you model stuff. The frequentist is assuming that you want to calculate the probability of observing a sample x given that the real paramater of the model is theta.
Hence, it makes the assumption that theta is deterministic, and hence, making probabilistic statement regarding theta are non-sense.
The Baysian always presumes a distribution for the parameter.
The two can be somewhat reconciled via what one would call a hierarchical model. Hence, the frequentist would also assume theta to be random, and another parameter (gamma) to be the deterministic one. This is similar to the Bayesian modeling.

The main weakness I see in the Bayesian interpretation comes from the "prior as a degree of belief", which is just bs to me. The weakness in frequentism is assume that parameters are deterministic, when in reality they mostly are not.