Introduction
This article aims to show how you can create a simple function in Julia to get the factorial of a given number.
What is factorial?
The product of all integers equal to or less in value than the original number — in other words, a factorial is the number of possible combinations with numbers less than or equal to that number.
We symbolise the factorial of a number with “!” (e.g. 4!).
Some examples
2!=2∙1=2
3!=3∙2∙1=6
4!=4∙3∙2∙1=24
Logical zero factorial proof
As we said, a factorial is the number of possible combinations with numbers less than or equal to that number. Zero has no numbers less than it, but it is a number itself. How many arrangements can I do with 0 items? None at all. This is too a way of arrangement, so 0!=1 (none).
Suppose we have three fruits:
🍎🍐🍊
What are the arrangements?
🍎🍐🍊
🍎🍊🍐
🍐🍎🍊
🍐🍊🍎
🍊🍎🍐
🍊🍐🍎
3!=6 as we said previously.
Think similarly for 0!.
Function in Julia
function f(n::Int64)
f = 1
if n < 0
print("Factorial does not exist for negative numbers")
end
if n == 0
print("The factorial of 0 is 1")
end
if n>0
for i in 1:n
f = f*i
end
println("The factorial is: ",f)
end
end
Let’s ask the factorial of -3 (n=-3)
f(-3)
Output:
Factorial does not exist for negative numbers
Let’s ask the factorial of 0 (n=0)
f(0)
Output:
The factorial of 0 is 1
Let’s ask the factorial of 3 (n=3)
f(3)
Output:
The factorial is: 6
Let’s explain the part of the code below:
for i in 1:n
f = f*i
end
Firstly, we defined the f as 1.
So, we start with f=1.
for i in 1:3
- f=1*1=1
- f=1*2=2
- f=2*3=6 end
That’s simple!
Conclusion
In this article, we gave a simple explanation of the factorial as well we made an easy function in Julia!
Thank you for reading!🤗
Article Cover Photo: Photo by Tommy Bond on Unsplash


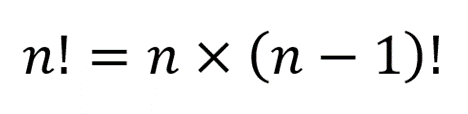

Top comments (2)
I liked this article - I wrote a similar one when I was starting out with Julia too!
And then a kind Teacher Assistant for my course came along (with a sneaky smile) and whispered something about some ternary operator...
...Which creeped me out.
Vexed me!
But not as much as when I found out about the world of map, reduce, and folds, and all those nifty iterator methods that can get you out of a pinch:
Add to the discussion