Julia in the class

This post will be in Spanish to encourage more Spanish speaking people to try and use julia

La idea de este post es mostrar como leer datos de un archivo .txt de un acelerómetro para luego utilizando una aproximación de la derivada, resolver numéricamente una ecuación diferencial.
El material corresponde a un curso corto que estoy preparando para estudiantes de segundo año en la Facultad de Ingenieria de la Universidad de Buenos Aires.

Para poder leer el archivo necesitamos que el mismo se encuentre en la misma carpeta donde estamos trabajando. El mismo se puede encontrar en el repo de Lorena Barba de donde sacamos la idea de este tutorial link

Antes que nada preparemos es espacio de trabajo

using Plots 
using DelimitedFiles
plotly()

Leemos los datos del archivo usando readlm y luego veremos qué forma tiene:

acelerometro = readdlm("therocket.txt")

acelerometro = 151×2 Matrix{Float64}:
  0.0   0.273164
  0.1   1.44111
  0.2   2.66931
  0.3   4.23838
  0.4   5.64995
  0.5   6.94892
  0.6   8.42349
  ⋮    
 14.5  -0.511472
 14.6  -0.387906
 14.7  -0.402696
 14.8  -0.138835
 14.9  -0.334849
 15.0   0.109764

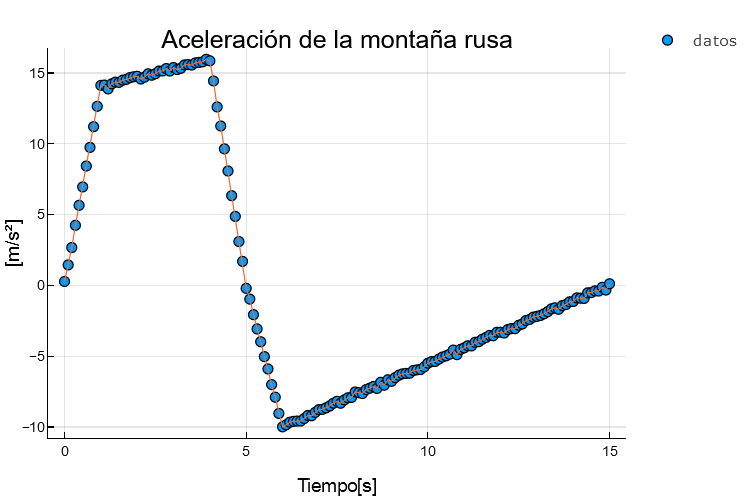
Podemos observar que los datos estan en una matriz de 151 filas y 2 columnas. La primer columna es el tiempo y la segunda la aceleración medida

Para poder trabajar de una manera más cómoda llamaremos t a la primer columna para referirnos al tiempo y a a la segunda para indicar la aceleracion. acelerometro[:,1] son todos los valores de la columna 1 es decir nuestra t y acelerometro[:,2] son los de la columna 2 , siendo los valores de a

t, a  = acelerometro[:,1] , acelerometro[:,2]; 
# Chequeemos que tipo de dato nos da `t` 
typeof(t) 
Vector{Float64} (alias for Array{Float64, 1})

Si queremos conocer cuantos elementos tiene el vector (en realidad ya lo sabemos porque al leer los datos del acelerometro nos aparecio un 151×2 Matrix{Float64}: lo que significa que es un elemento de 151 filas y 2 columnas) podemos utilizar la siguiente función:length(vector_que_usemos). Veamos que nos dice con el tiempo (en realidad ya lo sabiamos de antes pero no está de más chequearlo

length(t)
151

Perfecto, manos a la obra. Ahora vamos a graficar los puntos que obtuvimos.

scatter(t,a,label="datos")
    plot!(t,a,label="")
    title!("Aceleración de la montaña rusa")
    xlabel!("Tiempo[s]")
    ylabel!("[m/s²]")

Bien, con esto ahora vamos a obtener la velocidad y posicion del carrito de la montaña rusa utilizando el famoso y mejor amigo del ingeniere, y me pongo de pie... Polinomio de Taylor

Sabemos que la velocidad es la derivada de la posicion respecto al tiempo y lo mismo con la aceleración donde esta es la derivada de la velocidad respecto al tiempo:

$\begin{aligned} v(t_i) = \frac{dx}{dt} \space a(t_i) = \frac{dv}{dt} \end{aligned}$

Usando la definicion de derivada a pártir del coeficiente incremental tenemos :

$v(t_i) = \frac{dx}{dt} \approx \frac{x(t_i+\Delta t)-x(t_i)}{\Delta t}$

y para la aceleracion

$a(t_i) = \frac{dv}{dt} \approx \frac{v(t_i+\Delta t)-v(t_i)}{\Delta t}$

Entonces si queremos encontrar la velocidad podemos escribir

$v(t_i+\Delta t) \approx v(t_i) + a(t_i) \Delta t$

Osea que si queremos conocer la velocidad en un momento $t_i+\Delta t$ , simplemente aplicamos la ecuacion de arriba. Importante, estamos suponiendo que partimos del reposo, osea que nuestra velocidad inicial es nula.

Esto en código se va a ver de la siguiente forma:

velocidad[tiempo t+ Δt] = velocidad[tiempo t] + aceleracion[tiempo t] * dt

Para poder escribirlo, necesitamos saber el dt, como estamos trabajando con puntos esto se puede obtener de la forma:

dt = (algun tiempo) - (algun tiempo - 1)

dt = t[2] - t[1] 
dt= 0.1

Para comenzar vamos a inventar dos vectores de ceros y luego con un for vamos calculando la velocidad

v = zeros(length(a))
x = zeros(length(a))

Ahora si hacemos el cálculo

for i in 1:length(v)-1
    v[i+1] = v[i] + a[i] * dt
    x[i+1] = x[i] + v[i] * dt
end

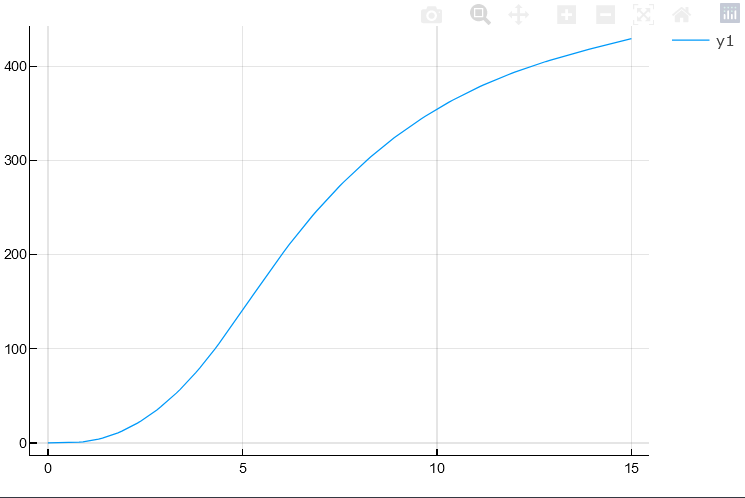
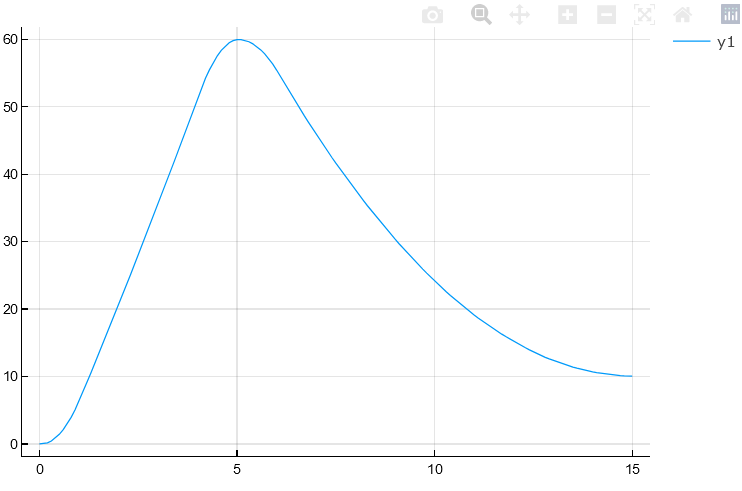
Hagamos un primer gráfico rápido para chequear la forma de la posicion respecto al tiempo y luego repetimos con la velocidad

plot(t,x) 

plot(t,v) 

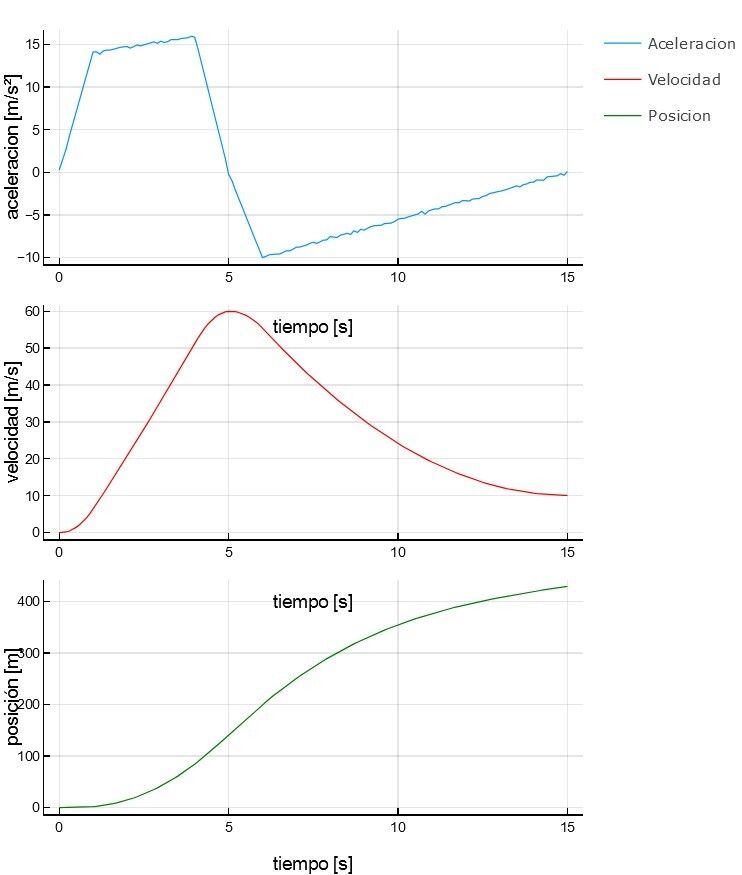
Ahora ponemos los tres graficos bien lindos y juntos

        grafico1 = plot(t,a,label="Aceleracion",xlabel="tiempo                                  [s]",ylabel="aceleracion [m/s²]")
    grafico2 = plot(t,v,label="Velocidad",xlabel="tiempo [s]",ylabel="velocidad [m/s]",c=:red)
    grafico3 = plot(t,x,label="Posicion",xlabel="tiempo [s]",ylabel="posición [m]",c=:green)

    plot(grafico1,grafico2,grafico3, layout=(3,1),size=(600, 700))

Espero que con esta pequeña introducción más gente descrubra este hermoso lenguaje
Proximamente una versión en inglés

Para este apunte nos basamos del trabajo de Lorena Barba en Engineering Computations

Barba, L.A., 2020. Engineers Code: reusable open learning modules for engineering computations. Computing in Science & Engineering, 22(4), pp.26-35. doi:10.1109/MCSE.2020.2976002 Preprint on arXiv::2001.00228