Let me explain how to make a square matrix with integer entries so that its inverse contains only integer entries. This kind of matrices might be useful for demonstrating Gaussian-Jordan elimination for solving a linear system without any fractions coming up in between.
The Sherman-Morrison formula is given by
,
where
is an invertible matrix of order
and
and
are column vectors of size
.
Ref : Sherman–Morrison formula - Wikipedia
Let and in .The vectors and are orthogonal.
If , then . We can notice that if entries of both and are integers then entries of both and will be integers. This could be useful for designing a consistent linear system with integer coefficient matrix. If the constant vector contains only integer entries, then the solution also contains only integer entries. Integer matrices with integer inverses are called unimodular matrices. The determinant of will be 1.
Let
and . It can be verified that .
Then
The resulting linear system can be written as (with )
Now the Gauss-Jordan elimination can be applied to the above linear system to get a unique solution as
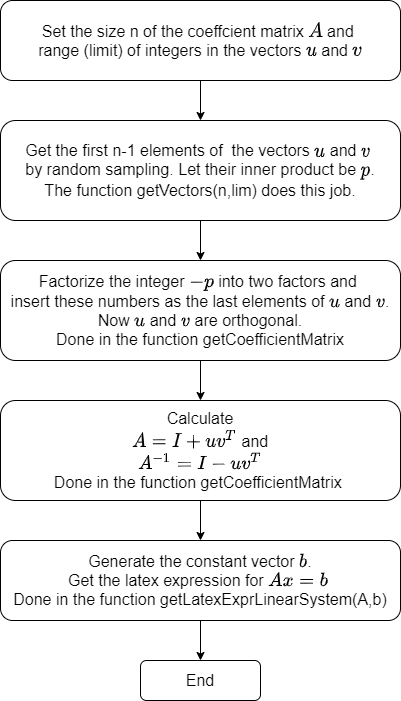
I have coded to make unimodular matrices in Julia. The flowchart of the program is given below.
using LinearAlgebra
using Primes
function getVectors(n,lim)
#get the first n
global u,v,p
while true
u = rand(-lim:lim,n,1)
v = rand(-lim:lim,n,1)
println("u = ",u)
println("v = ",v)
p = u'*v
if 0 == p
continue
end
if abs(p[1]) > 0
break
end
end
return u,v,p
end
function getCoefficientMatrix(n,lim)
#Return two matrices: A and its inverse Ainv
#Coefficient matrix A such that A = I + uv^T
#Ainv = I - uv^T
#lim = 5
#get random column vectors u and v whose elements are in the range [-lim,lim]
#p is the inner product of u and v, p = u^T v.
u,v,p = getVectors(n,lim)
println("p = u^T v = ",p[1])
#Add one more element to u and v such that the resulting vectors are orthogonal.
#Factorize p[1] into two numbers factor1 and factor2
mult = 1
if p[1] > 0
mult = -1
end
factors = factor(Vector,p[1]) #from the Primes package
println("Factors of p are ")
println(factors)
switches = rand([true,false],length(factors))
if length(factors) > 1
switches[1:2] .= [true,false]
end
factor1 = 1
factor2 = 1
k = 1
for f in factors
if true == switches[k]
factor1 *= f
else
factor2 *= f
end
k = k + 1
end
factor1 *= mult
println("factor1 = ",factor1)
println("factor2 = ",factor2)
#Append last element to u and v
u = vcat(u,factor1)
v = vcat(v,factor2)
#Now u and v are orthogonal
println("u = ",u)
println("v = ",v)
println("u'*v = ",u'*v)
A = I + u*v'
Ainv = I - u*v'
return A,Ainv
end
function getLatexExprLinearSystem(A,b)
m,n = size(A)
stri = "\$"
for i in 1:m
stri *= join([string(A[i,j])*"x_"*string(j) for j in 1:n], " + ")
stri *= " = " * string(b[i])
if m == i
stri *= "\$\n"
else
stri *= "\$\n\$"
end
end
stri = replace(stri,"+ -"=>" - ")
stri = replace(stri,"+ 1" => "+ ")
stri = replace(stri,".0x" => "x")
stri
end
n = 4 #Size of the linear system
limit = 4 #Approximate range of integers in the vectors u and v
A,Ainv = getCoefficientMatrix(n-1,limit)
println("The coefficient matrix A is")
display(A)
println("The inverse of coefficient matrix A is")
display(Ainv)
b = rand(-10:10,n) #the constant vector b of Ax = b
s = getLatexExprLinearSystem(A,b)
println("Latex expression for the linear system is :")
print(s)
println("The solution for the linear system is :")
display(Ainv*b)


Oldest comments (0)